Inequality Expressions

Key Questions

What are the different inequality notations?

There are four inequality notations. They are

#># means greater than

#>=# means greater than or equal to

#<# means less than

#<=# means less than or equal to

Meave60 · 1 · Dec 23 2014
What are Inequalities?

They are basically regular functions, but instead of equal signs, they use a variant of less than ">" or greater than "<" in place of the equal sign.

To keep things simple, refer to the function:

#y=2x+3#

It is a basic line. Whatever you plug in a value x, it must fulfill a value for y. If x=1, y must equal 5.

Then you have inequalities.

#y>=2x+3#

Basically, every value for x and y above or on the line will work as an answer. The point (0, 4) is a good answer, because:

#4>=2(0)+3#
#4>=3#

#y<=2x+3#

Because this is #y<=f(x)#, every value of x and y below or on the line will work as an answer. (0, 0) works because:

#0<=2(0)+3#
#0<=3#

Finally there are the non-equal inequalities:

#y<2x+3#
#y>2x+3#

Like the previous inequalities, greater than is anything above the line and less than is anything below the line. The main difference? Anything on the line is not an answer.

Referring to point (1,5)
#5< or>2(1)+3#
#5< or >5#
Is false.

Once you remove the "or equal" part, the entire line is not an answer. On a graph, this line is usually dotted to mean that the line is not an answer, but just a boundary on what can be an answer.

Joe O. · 2 · Nov 19 2014
How do you graph an inequality on a number line?

Inequalities represent a range of values, rather than a single value.

Let's see some examples to understand better.

Let us consider the inequality
#x>2#

This would mean #x# can be any value greater than #2#, not including #2#.

This is represented by a line starting from #2#, and extending indefinitely (marked by an arrow head). Note that at #2#, there is a small empty circle which represents that #2# is not included.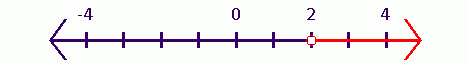

In case the inequality was
#x>=2#

It would mean that #2# has also been included. Thus, the small circle on 2 would be filled, as: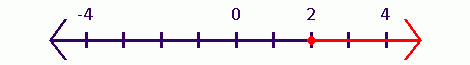

In case you can't draw on the number line, you can also show the range just above the number.

If your inequality is
#5>x>=-2#

You can represent it as:

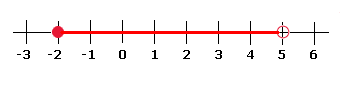
Following are some great examples that I got from here.

Tanish J. · 1 · Nov 28 2014
How does a linear inequality different from a linear equation?

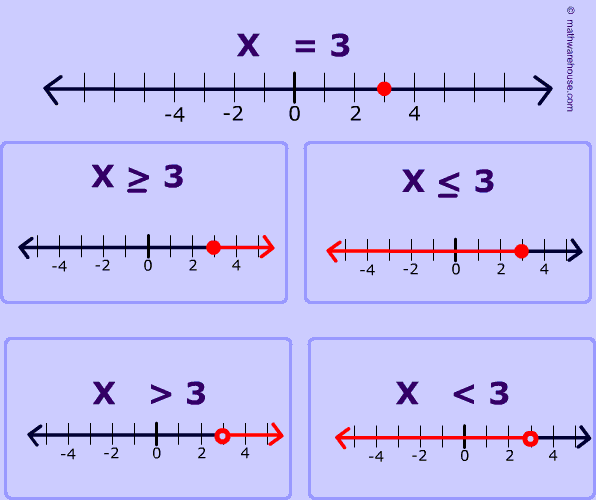
Answer:

A linear equation will have one solution where as a linear inequality can have numerous.

Explanation:

E.g. #3x+4=7 =>x=1# only one solution
But #3x+4>7 => x>1# every number larger than one is a correct solution.

Mark D. · 1 · May 9 2018