How many electrons in an atom can have #n=7# and #m_l = +3# ?
1 Answer
Explanation:
The trick here is to focus on the value of the magnetic quantum number,
You know that every value the magnetic quantum number takes represents an orbital. You also know that every orbital can hold a maximum of
You can thus say that
#m_l = +3#
can be shared by a maximum of
Now, we use a total of four quantum numbers to describe the position and spin of an electron inside an atom.
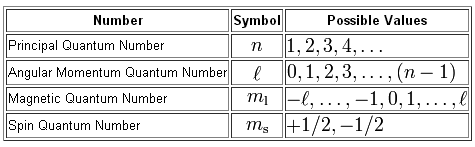
As you can see, the value of the magnetic quantum number depends on the value of the angular momentum quantum number,
More specifically, you know that
#m_l = {-l, -(l-1),..., -1, color(white)(-)0, +1, ..., (l-1), l}#
and that
#l = {0, 1, ..., n-1}#
For
#l = {0, 1, 2, 3, 4, 5, 6}#
Notice that you can only have
#l = {color(red)(cancel(color(black)(0, 1, 2))), 3, 4, 5, 6}#
You can thus say that you have
#l = 3#
#m_l = {-3,-2,-1,0,+1,+2,color(red)(+3)}#
#l = 4#
#m_l = {-4, -3,-2,-1,0,+1,+2,color(red)(+3), +4}#
#l = 5#
#m_l = {-5, -4, -3,-2,-1,0,+1,+2,color(red)(+3), +4, +5}#
#l = 6#
#m_l = {-6, -5, -4, -3,-2,-1,0,+1,+2,color(red)(+3), +4, +5, +6}#
So, you know that for
#4 color(red)(cancel(color(black)("orbitals"))) * "2 e"^(-)/(1color(red)(cancel(color(black)("orbital")))) = "8 e"^(-)#
Therefore, you know that a maximum of
#n=7, m_l = +3#

