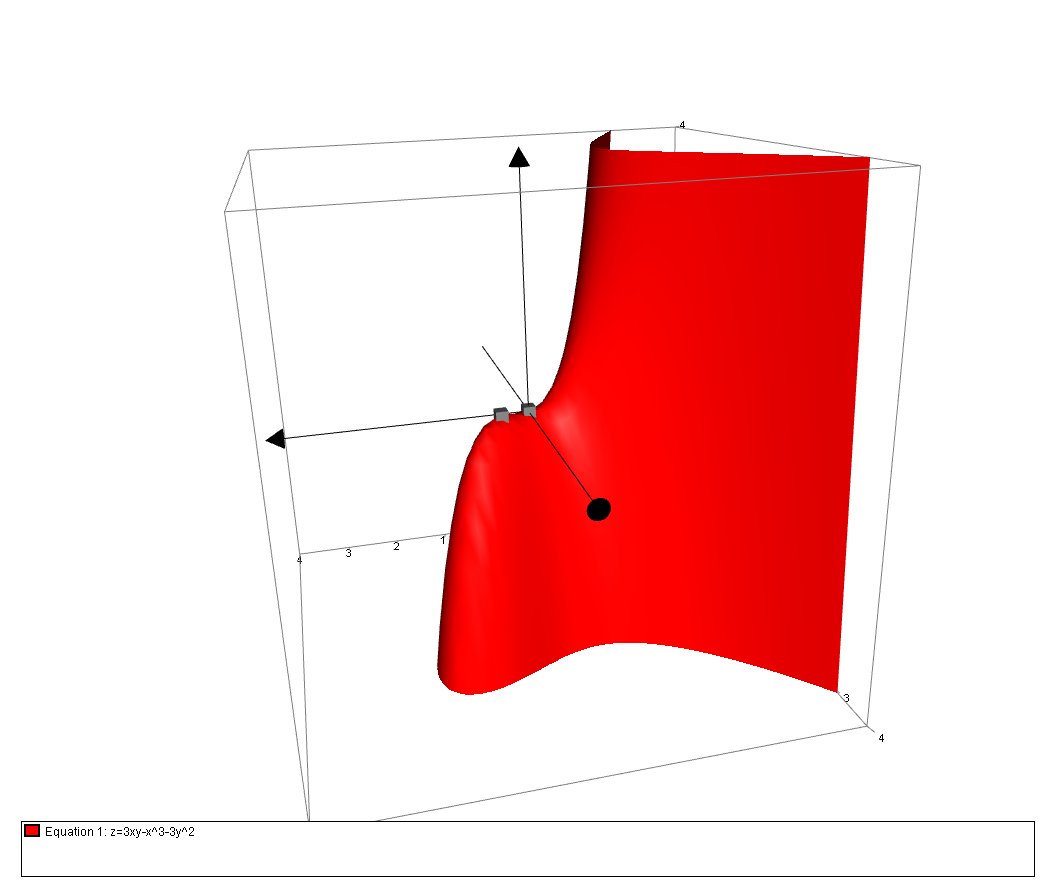
Identify the Critical Points for the function? : # f(x,y) = 3xy-x^3-3y^2 #
2 Answers
The saddle point is
Explanation:
Our function is
The partial derivatives are
We look for the critical points
We solve for
Therefore, the critical points are
Therefore,
To perform the second derivative test, we calculate the determinant,
# (0,0) # - Saddle Point
# (1/2,1/4) # - Maximum
Explanation:
We have:
# f(x,y) = 3xy-x^3-3y^2 #
Step 1 - Find the Partial Derivatives
We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:
The First Derivatives are:
# f_x \ = (partial f) / (partial x) \ \ = 3y -3x^2 #
# f_y \ = (partial f) / (partial y) \ \ = 3x-6y #
The Second Derivatives are:
# f_(x x) =(partial^2 f) / (partial x^2) = -6x #
# f_(yy) = (partial^2 f) / (partial y^2) = -6 #
The Second Partial Cross-Derivatives are:
# f_(xy) =(partial^2 f) / (partial x partial y) =3 #
# f_(yx) = (partial^2 f) / (partial y partial x) =3 #
Note that the second partial cross derivatives are identical due to the continuity of
Step 2 - Identify Critical Points
A critical point occurs at a simultaneous solution of
# f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0#
i.e, when:
# 3y -3x^2 = 0# ..... [A]
# 3x-6y \ \ = 0 # ..... [B]
From [A] we have:
# 3x-6x^2 = 0 => 2x^2-x =0 #
# :. x(2x-1) = 0 #
# :. x=0,1/2 #
And the using
# x=0 \ \ => y = 0 #
# x=1/2 => y = 1/4 #
So we can conclude that there are two critical points:
# (0,0) # ; and# (1/2,1/4) #
Step 3 - Classify the critical points
In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.
# Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2 #
Then depending upon the value of
# {: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :} #
Using custom excel macros the function values along with the partial derivative values are computed as follows: