Question

A sheet in the shape of a sector of radius `40cm.` and angle `26^@` is cut. Now answer the following?

(a)(i) What is the area of the sector?
(a) (ii) What is the length of its arc?
(b) (i) If the sector is folded to form a cone, what is the radius of base of the cone?
(b) (ii) What is the capacity of this cone?

Answer 1

Please see below.

Explanation:

We know that area of a circle is `pir^2`. Now as circle makes an angle `360^@`, area of a sector is `pir^2xxA/360^@`, where `A`is the angle of the sector in degrees.

(a) (i) Hence area of the sector is `3.1416xx40^2xx26/360=363.03` `cm^2`

(a) (ii) the length of the arc similarly would be `26/250` of circumference, which is `2pir`. Hence length of arc is `2xx3.1416xx40xx26/360=18.15` `cm.`

(b) (i) As the sector when folded forms an inverted right cone, its arc form a complete circle as shown below.

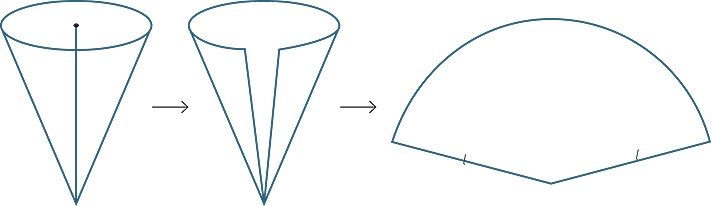
Hence if `a` is the radius, we have `2pia=18.15` or `a=18.15/(2xx3.1416)=2.89` `cm.`

(b) (ii) The radius of earlier arc forms slant height and this `40` `cm` and radius of cone is `2.89` `cm.`. Hence vertical height is `sqrt(40^2-2.89^2)=sqrt(1600-8.35)=sqrt1591.65=39.9` `cm.`

(c) The capacity of the cone is given by its volume i.e. `1/3pir^2h` and hence is `1/3xx3.1416xx2.89^2xx39.9=349` `cm^3` or `349/1000=0.349` litres