A farmer has a rectangular property that needs to be fenced on three sides (a river surrounds the fourth. If he has 2400 feet of fencing material available, what maximum area will he be able to enclose?
1 Answer
The dimensions that give the maximum area are
Explanation:
Start by tracing a diagram.
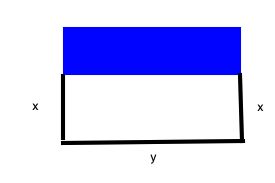
We now have:
2x + y = 2400
If we solve for
y = 2400 - 2x
Now, we know that
A = (2400 - 2x)x
A = -2x^2 + 2400x
Now differentiate with respect to
(dA)/(dx) = -4x + 2400
Find critical numbers.
0 = -4x + 2400
x = 600
Since
Therefore, the dimensions the give the maximum area are
We know that this is a maximum because the function
Hopefully this helps!


