The density is #"28.9 g/cm"^3#.
Calculate the mass of the unit cell

An fcc unit cell contains
#8 color(red)(cancel(color(black)("corners"))) × (1/8 "atom")/(1 color(red)(cancel(color(black)("corner")))) + 6 color(red)(cancel(color(black)("faces"))) × (1/2 "atom")/(1 color(red)(cancel(color(black)("face")))) = "1 atom + 3 atoms = 4 atoms"#
#"Mass" = 4 color(red)(cancel(color(black)("atoms"))) × (1 color(red)(cancel(color(black)("mol"))))/(6.022 × 10^23 color(red)(cancel(color(black)("atoms")))) × "114 g"/(1 color(red)(cancel(color(black)("mol")))) = 7.57 ×10^"-22"color(white)(l) "g"#
Calculate the volume of the unit cell
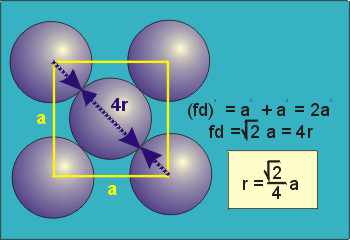
The diagonal along a face is #d = 4r#.
#d^2 = a^2 + a^2 = 2a^2 = (4r)^2 = 16 r^2#
#a^2 = 8r^2#
#a = rsqrt8 = sqrt8 × 105 × 10^"-12" color(red)(cancel(color(black)("m"))) × "100 cm"/(1 color(red)(cancel(color(black)("m")))) = 2.97 × 10^"-8" color(white)(l)"cm"#
#V = a^3 = (2.97 × 10^"-8" color(white)(l)"cm")^3 = 2.62 × 10^"-23"color(white)(l) "cm"^3#
Calculate the density
#ρ = m/V = (7.57 ×10^"-22"color(white)(l) "g")/(2.62 × 10^"-23"color(white)(l) "cm"^3) = "28.9 g/cm"^3#



