Question

Question #17b01

Answer 1

Here's what I got.

Explanation:

You're dealing with the beta minus decay of neptunium-238.

In beta minus decay, a neutron located inside the nucleus of a radioactive nuclide is being converted to a proton. The process releases an electron, also called a beta particle, and an electron antineutrino, `bar(nu)_e`.

`color(white)(a)`

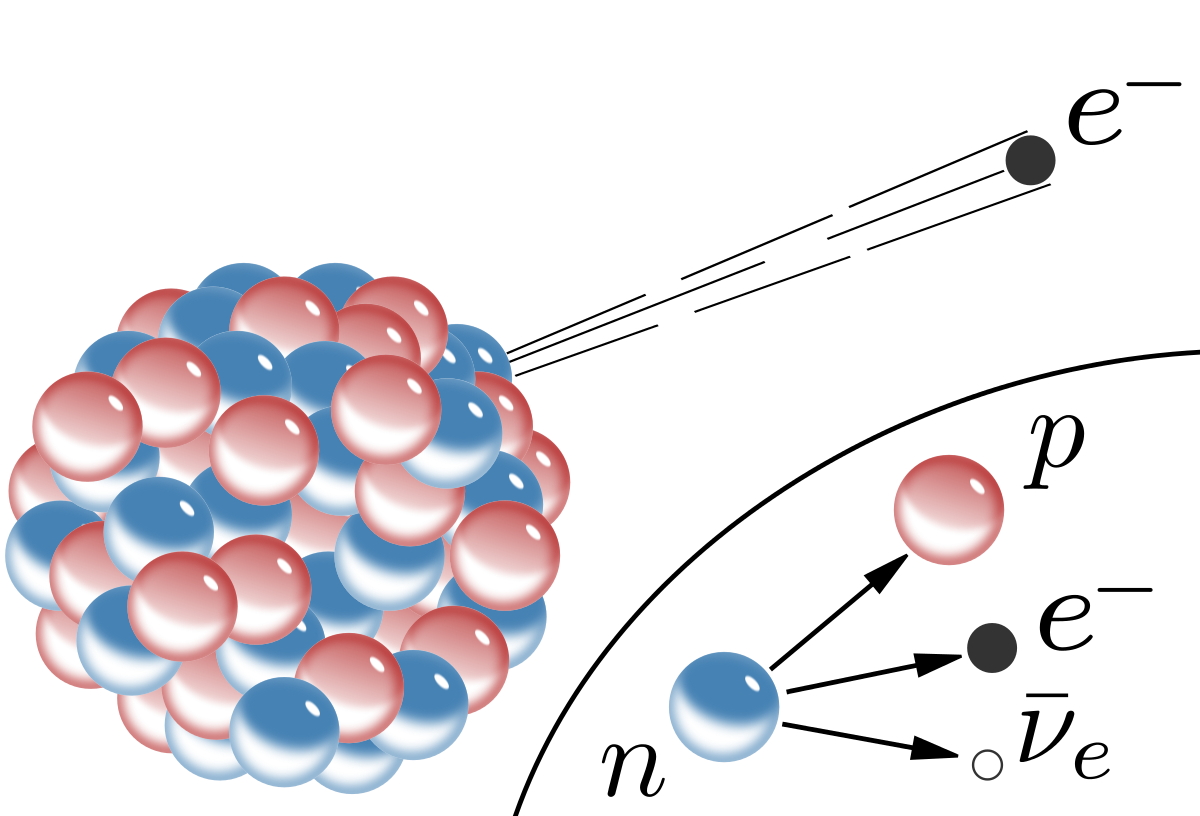
So, you know that you're starting with

`""_ (color(white)(1)color(darkgreen)(93))^color(blue)(238)"Np" -> ""_ color(darkgreen)(Z)^color(blue)(A)"?" + ""_ color(darkgreen)(-1)^(color(white)(-)color(blue)(0))"e" + bar(nu)_e`

Your goal here is to figure out the values of `A` and `Z`, the mass number and the atomic number, respectively, of the resulting nuclide.

As you know, mass and charge must be conserved in nuclear equations. This means that you can write

`color(darkgreen)(93 = Z + (-1)) ->` conservation of charge

`color(blue)(238 = A + 0) color(white)(aaa)->` conservation of mass

You can thus say that

`Z = 93 + 1 = 94" "` and `" "A = 238`

Grab a Periodic Table and look for the element that follows neptunium. You'll find that this element is plutonium, `"Pu"`. The resulting nuclide is plutonium-238.

You can now complete the nuclear equation that describes the beta minus decay of neptunium-238

`""_ (color(white)(1)color(darkgreen)(93))^color(blue)(238)"Np" -> ""_ (color(white)(1)color(darkgreen)(94))^color(blue)(238)"Pu" + ""_ color(darkgreen)(-1)^(color(white)(-)color(blue)(0))"e" + bar(nu)_e`