The calculations are tedious but not difficult.
The balanced equation is
#"NaOH + HCl" → "NaCl" + "H"_2"O"#
pH at start
#["OH"^"-"] = "0.007 25 mol/L"#
#"pOH" = "-log"("0.007 25") = 2.14#
#"pH = 14.00 - pOH = 14.00 - 2.14 = 11.86"#
pH at equivalence point
#color(blue)(bar(ul(|color(white)(a/a)c_text(A)V_text(A)= c_text(B)V_text(B)color(white)(a/a)|)))" "#
#V_text(A) = V_text(B) × c_text(B)/c_text(A) = "690 mL" × ("0.007 25" color(red)(cancel(color(black)("mol/L"))))/(0.10 color(red)(cancel(color(black)("mol/L")))) = "50.0 mL"#
The equivalence point is at 50.0 mL #"HCl"#.
pH at 25 mL
At this point, you have neutralized half the moles of #"NaOH"#.
#"Initial moles" = 0.690 color(red)(cancel(color(black)("L NaOH"))) × ("0.007 25 mol NaOH")/(1 color(red)(cancel(color(black)("L NaOH")))) = "0.005 00 mol"#
#"Moles present" = 0.5 × "0.005 00 mol" = "0.002 500 mol"#
#"Volume = (690 + 25) mL = 715 mL = 0.715 L"#
#["OH"^"-"] = "0.002 500 mol"/"0.715 L" = "0.003 50 mol/L"#
#"pOH = -log(0.003 50) = 2.46"#
#"pH = 14.00 - 2.46 = 11.54"#
pH at 49 mL
#"Moles reacted" = 49/50 × "0.005 00 mol" = "0.004 90 mol"#
#"Moles present" = "(0.005 00 -0.004 90) mol" = "0.000 10 mol"#
#"Volume = (690 + 49) mL = 739 mL = 0.739 L"#
#["OH"^"-"] = "0.000 10 mol"/"0.739 L" = "0.000 135 mol/L"#
#"pOH = -log(0.000 135) = 3.87"#
#"pH = 14.00 - 3.87 = 10.13"#
pH at 49.9 mL
#"Moles reacted = 49.9/50.0 × "0.005 00 mol" = "0.004 99 mol"#
#"Moles present" = "(0.005 00 -0.004 99) mol" = "0.000 01 mol"#
#"Volume = (690 + 49.9) mL = 739.9 mL = 0.7399 L"#
#["OH"^"-"] = "0.000 01 mol"/"0.7399 L" = "0.000 014 mol/L"#
#"pOH = -log(0.000 014) = 4.87"#
#"pH = 14.00 - 4.87 = 9.13"#
After the equivalence point, you have neutralized all the #"NaOH"# and have a solution of excess #"HCl"#.
pH at 50.1 mL
#"Moles HCl added" = 0.0501 color(red)(cancel(color(black)("L"))) × "0.10 mol"/(1 color(red)(cancel(color(black)("L")))) = "0.005 01 mol"#
#"Excess moles HCl = (0.005 01 - 0.005 00) mol = 0.000 01 mol"#
#"Volume = (690 + 50.1) mL = 740.1 mL = 0.7401 L"#
#"[HCl]" = "0.000 01 mol"/"0.7401 L" = "0.000 014 mol/L"#
#"pH = -log(0.000 013) = 4.87"#
pH at 51 mL
#"Moles HCl added" = 0.051 color(red)(cancel(color(black)("L"))) × "0.10 mol"/(1 color(red)(cancel(color(black)("L")))) = "0.0051 mol"#
#"Excess moles HCl = (0.0051 - 0.005 00) mol = 0.0001 mol"#
#"Volume = (690 + 51) mL = 741 mL = 0.741 L"#
#"[HCl]" = "0.0001 mol"/"0.741 L" = "0.000 13 mol/L"#
#"pH = -log(0.000 13) = 3.87"#
pH at 75 mL
#"Moles HCl added" = 0.0750 color(red)(cancel(color(black)("L"))) × "0.10 mol"/(1 color(red)(cancel(color(black)("L")))) = "0.007 50 mol"#
#"Excess moles HCl = (0.007 50 - 0.005 00) mol = 0.002 50 mol"#
#"Volume = (690 + 75) mL = 765 mL = 0.765 L"#
#"[HCl]" = "0.002 50 mol"/"0.741 L" = "0.003 27 mol/L"#
#"pH = -log(0.00 327) = 2.49"#
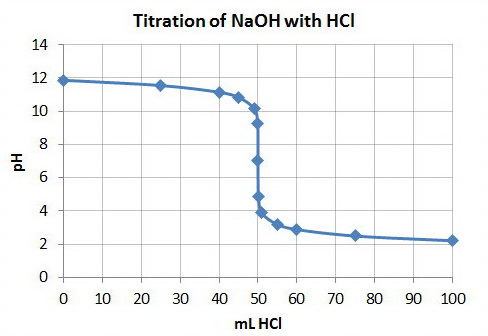
Plot pH vs Volume
Plot the points on a graph and draw a smooth curve between them.
I added a few extra points to get a smoother curve.
Your graph should something like this.