Question

Question #8f60c

Answer 1

Thermometer Y shows a temperature of 24 °Y.

Explanation:

To help us work through this problem, I adapted an image of two common thermometer scales.

Ignore the markings on the thermometers and look at the markings outside them.

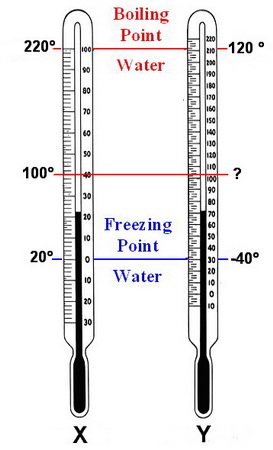
(Adapted from www.tf.uni-kiel.de)

On Thermometer X,

`T_text(boil) - T_text(freeze) = "220 ° - 20 ° = 200 °"`

On Thermometer Y,

`T_text(boil) - T_text(freeze) = "120 ° - (-40 °) = 160 °"`

∴ `"200 X° = 160 Y °"`

A temperature of 100 °X is 80 X° above the freezing point of water.

`80 color(red)(cancel(color(black)("X°"))) × "160 Y°"/(200 color(red)(cancel(color(black)("X°")))) = "64 Y°"`

The temperature is 64 Y° above the freezing point of water.

∴ On Thermometer Y,

`T = "-40 ° + 64 ° = 24 °"`

Hence, `"100 °X = 24 °Y"`