When adding base to a weak acid, does the concentration of #"HA"# have a net increase after the endpoint?
2 Answers
I assume you mean adding strong base to a weak acid.
At the endpoint (i.e. the inflection point in the graph, the equivalence point), ALL of the weak acid
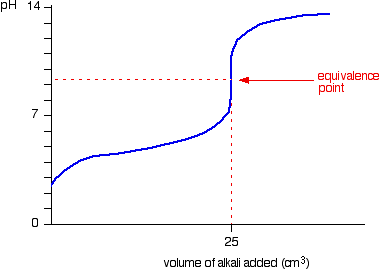
So no, the concentration of acid
AFTER THE END POINT, BEFORE LEVEL-OFF
If you bothered to check Le Chatelier's principle at the endpoint, the generated weak conjugate base
(This would be at, say,
#"A"^(-)(aq) + "H"_2"O"(l) rightleftharpoons "HA"(aq) + "OH"^(-)(aq)#
Adding more strong base (say,
Hence, the concentration of weak acid tries to increase but gets neutralized as it gets generated.
This is presented as alternate context to the original answer which is 100% correct. Just offering a different point of view.
The increase in wk acid beyond an equivalent reaction mixture of acid and base is 'insignificant' and pH increases should be assumed to be exclusively due to additional
Explanation:
Consider the reaction of one equivalent of acid and one equivalent of base. This produces one equivalent of salt + water and is the equivalent point of the titration. If the conjugate base of the salt is strong enough to abstract a proton from water (hydrolysis), then a weak acid is formed along with an excess of hydroxide ions.
The amount of acid formed by the hydrolysis reaction is equal to the excess hydroxide ions. This is such an insignificant amount of acid that it is generally assumed that additional titrant is solely responsible for pH increases without reaction up to the maximum pH of an alkaline system.
Example:
Given: 0.10M HOAc(aq) + 0.10M NaOH(aq) => 0.10M NaOAc(aq) + water
=>


