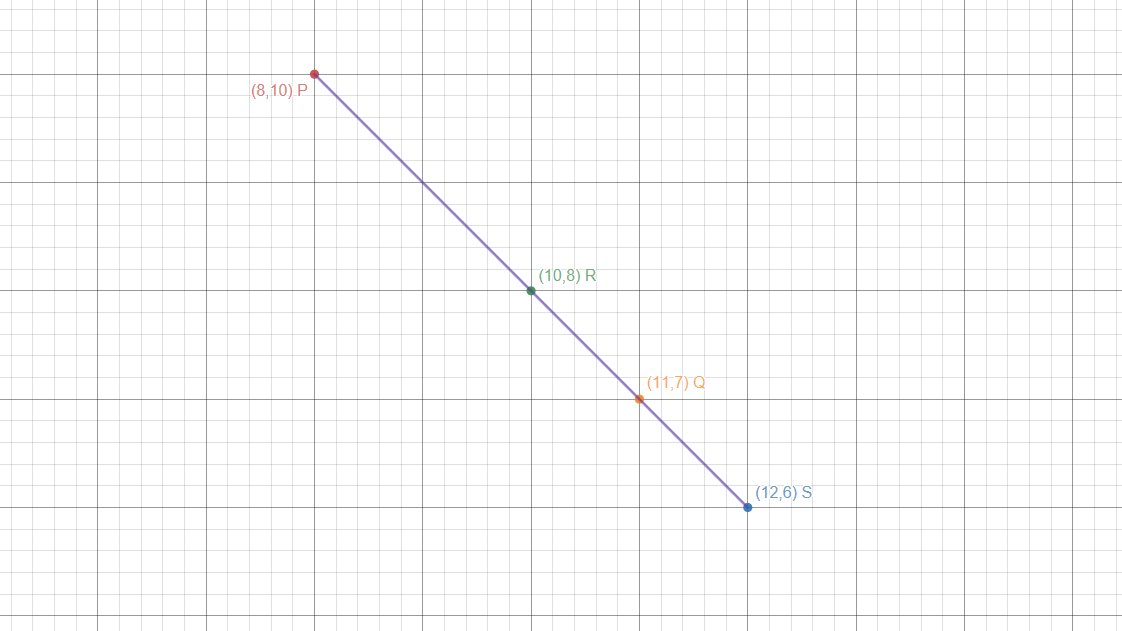
We can begin by plotting the points of the line segment #PS#. Since we know that #R# is the midpoint of the #PS# line segment, we can use the midpoint formula to find the coordinate of #R#
The midpoint formula: #((x_1+x_2)/2, (y_1+y_2)/2)#
Since we have our two coordinates of #P# and #S# we can substitute those values into the formula to find the coordinates of #R#
If we let, #(8,10)->(color(blue)(x_1),color(red)(y_1))# and #(12,6)->(color(blue)x_2,color(red)(y_2))# then.. .
#R= (color(blue)((8+12)/2), color(red)((10+6)/2))=(color(blue)(20/2),color(red)(16/2))=(color(blue)10,color(red)8)#
Since we now know the coordinates of #R# and already given #S# we can find the coordinate of #Q# since it is the midpoint of #RS#
By the same method above...
If we let, #(10,8)->(color(blue)(x_1),color(red)(y_1))# and #(12,6)->(color(blue)x_2,color(red)(y_2))# then.. .
#Q=(color(blue)((10+12)/2), color(red)((8+6)/2))=(color(blue)(22/2),color(red)(14/2))=(color(blue)11,color(red)7)#
So the coordinate of #Q# lies at #(11,7)# which is also the midpoint of line segment #RS#
Here is a graph to provide a visual representation of what I just explained.
If the image is to small, you can check the link below to this graph: https://www.desmos.com/calculator/vtaiir6ro8


