Midpoint Formula
Key Questions
-
Answer:
The coordinate of Midpoint
#:((x_1+x_2)/2, (y_1+y_2)/2)# Explanation:
#"If "A(x_1,y_1) and B(x_2,y_2) " are the two point on the line ,"# #"then midpoint M of the line segment " bar(AB) " is :"# #M((x_1+x_2)/2, (y_1+y_2)/2)# Please see the image.
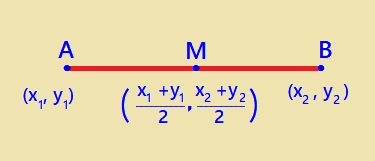
-
Answer:
You find the midpoint in exactly the same way with integers and fractions.
Explanation:
You find the midpoint in exactly the same way with integers and fractions, no matter whether they are common fractions, improper fractions or decimal fractions.
Add the two
#x# - values together and divide by#2# Add the two
#y# -values together and divide by#2# This will give a point,
#M(x,y)# -
If you know one endpoint
#(x_1,y_1)# and the midpoint#(a,b)# , but you do not know the other endpoint#(x_2,y_2)# , then by rewriting the midpoint formula:#{(a={x_1+x_2}/2 Rightarrow 2a=x_1+x_2 Rightarrow x_2=2a-x_1),(b={y_1+y_2}/2 Rightarrow 2b=y_1+y_2 Rightarrowy_2=2b-y_1):}# So, the unknown endpoint can be found by
#(x_2,y_2)=(2a-x_1,2b-y_1)#
I hope that this was helpful.
-
The midpoint
#M# of the points#(x_1,y_1)# and#(x_2,y_2)# is found by#M=({x_1+x_2}/2,{y_1+y_2}/2)# .As you can see above, the each coordinate of
#M# is the average of the corresponding coordinates of the endpoints.
I hope that this was helpful.
Questions
Radicals and Geometry Connections
-
Graphs of Square Root Functions
-
Simplification of Radical Expressions
-
Addition and Subtraction of Radicals
-
Multiplication and Division of Radicals
-
Radical Equations
-
Pythagorean Theorem and its Converse
-
Distance Formula
-
Midpoint Formula
-
Measures of Central Tendency and Dispersion
-
Stem-and-Leaf Plots
-
Box-and-Whisker Plots