Question

Question #7bc46

Answer 1

It's not always. If the distance at which the electric field or potential is evaluated is much bigger than the length of the dipole, then yes.

Explanation:

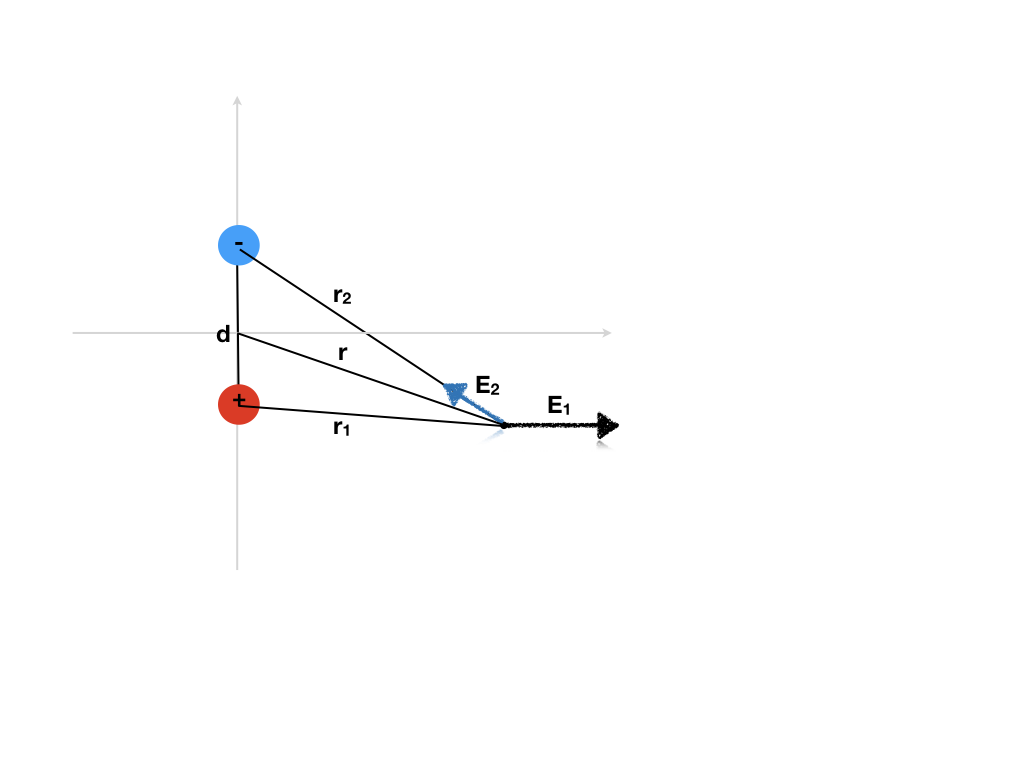
The dipole field at a point located at `vec r` away from the origin set at the center of a dipole is:

`vec E = vecE_1+vecE_2`

`vec E = (kqvecr_1)/r_1^3 - (kqvecr_2)/r_2^3`

Given q and d, if you know `vecr_1 and vecr_2`, you can readily calculate the dipole field or potential. In fact, that is what the computer is good at. Tell the computer a point , it is a breeze for it to compute the field using the equation above.

However, for us mortal, it's more convenient to assign
`vec r_1 = vecr- vecd/2`
and
`vec r_2 = vecr + vecd/2`

where `vecr` is from the center of the dipole and `vecd` is dipole length vector. This will make mathematical formulation manageable and easier to comprehend because `vec r_1 and vec r_2` are transformed into the dipole length and distance from the center of the dipole.

This transformation is particular useful when r >> d, because at that distance,
`r_1~~r_2~~r`

Hence, near the dipole, the field is fact not calculated by the distance from the center, but by distance from both charges. At distance far way, the distance from the center of the dipole is a good approximation for calculating the field or potential.