Question

Question #fb65f

Answer 1

I tried this but check my maths anyway....

Explanation:

Here you have various processes:
First steam cools down to `100^@`; then it condenses into water and then water is cooled down to `40^@` releasing a total amount of Energy/Heat, `Q_"tot"`:

We can change into grams `2kg=2000g` and write:

`Q_"tot"=Q_1+Q_2+Q_3`

`Q_"tot"=2000*2|100-174|+2000*2258+2000*4.18|40-100|=5,313,600J`

I used the absolute value to avoid confusion; it is heat that goes out of the system and is considered conventionally negative (heat in=positive, heat out=negative) but I didn't want to confuse you so remember that it is heat released into the environment.

Answer 2

You should get 5320 kJ.

Explanation:

Here is a schematic cooling curve for water.

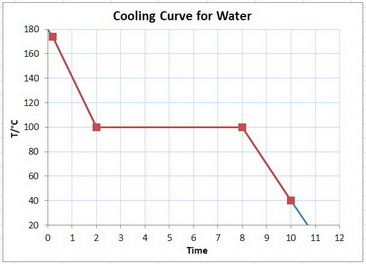
You are starting with the vapour at the top of the red graph, cooling it to 100 °C, condensing the steam along the horizontal line, and then cooling the water to the bottom of the red curve.

Thus, there are three separate heat removals involved in this problem:

• `q_1` = heat removed by cooling the steam from 174 °C to 100 °C
• `q_2` = heat removed by condensing the steam to water at 100 °C
• `q_3` = heat removed by cooling the water from 100 °C to 40 °C

`q = q_1 + q_2 + q_3 = mC_text(steam)ΔT_1 + nΔ_text(cond)H + mC_text(waterl)ΔT_3`

where

`mcolor(white)(mmm) = "the mass of the sample"`

`C_text(steam)color(white)(m) = "the specific heat capacity of steam"`

`C_text(water)color(white)(m) = "the specific heat capacity of water"`

`Δ_text(cond)H = "the enthalpy of condensation of steam"`

`ΔTcolor(white)(mm) = T_"f" -T_"i"`

`bbq_1`

`ΔT_1 = "100 °C - 174 °C = -74 °C"`

`q_1 = mC_text(steam)ΔT = 2000 color(red)(cancel(color(black)("g"))) × 2.010 color(white)(l)"J"·color(red)(cancel(color(black)( "°C"^"-1""g"^"-1"))) × ("-74" color(red)(cancel(color(black)("°C")))) = "-298 000 J" = "-298 kJ"`

`bbq_2`

`q_2 = mΔ_text(cond)H = 2000 color(red)(cancel(color(black)("g"))) × ("-2260 J"·color(red)(cancel(color(black)("g"^"-1")))) = "-4 520 000 J = -4520 kJ"`

`bbq_3`

`ΔT_3 = "40 °C - 100 °C = -60 °C"`

`q_1 = mC_text(water)ΔT = 2000 color(red)(cancel(color(black)("g"))) × 4.184 color(white)(l)"J"·color(red)(cancel(color(black)( "°C"^"-1""g"^"-1"))) × ("-60" color(red)(cancel(color(black)("°C")))) = "-510 000 J" = "-510 kJ"`

`q = q_1 + q_2 + q_3 = "(-298 - 4520 - 510) kJ" = "-5320 kJ"`

The process releases 5320 kJ of heat energy.