Question #73554
1 Answer
Explanation:
Start by taking a look at the balanced chemical equation that describes this reaction.
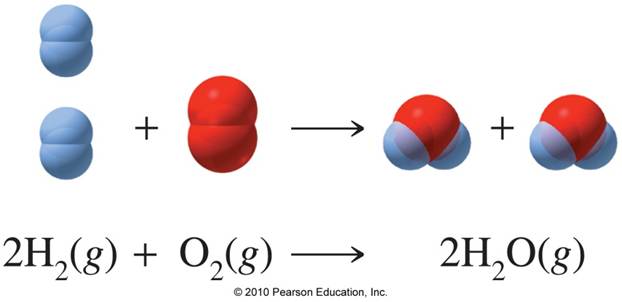
As you can see, every
Use the molar masses of the two reactants to convert the masses to moles
#4 color(red)(cancel(color(black)("g"))) * "1 mole H"_2/(2.0color(red)(cancel(color(black)("g")))) = "2 moles H"_2#
#20 color(red)(cancel(color(black)("g"))) * "1 mole O"_2/(32.0color(red)(cancel(color(black)("g")))) = "0.625 moles O"_2#
Now, you know that
Since you don't have enough moles of oxygen gas available, oxygen gas will act as a limiting reagent, i.e. it will be completely consumed before all the moles of hydrogen gas will get the chance to react.
This means that the reaction will consume
#0.625 color(red)(cancel(color(black)("moles O"_2))) * "2 moles H"_2/(1color(red)(cancel(color(black)("mole O"_2)))) = "1.25 moles H"_2#
and produce
#0.625 color(red)(cancel(color(black)("moles O"_2))) * ("2 moles H"_2"O")/(1color(red)(cancel(color(black)("mole O"_2)))) = "1.25 moles H"_2"O"#
To convert the number of moles to grams, use the molar mass of water
#1.25 color(red)(cancel(color(black)("moles H"_2"O"))) * "18.015 g"/(1color(red)(cancel(color(black)("mole H"_2"O")))) = color(darkgreen)(ul(color(black)("20 g")))#
The answer must be rounded to one significant figure, the number of sig figs you have for your values.

