How does the average kinetic energy of a system change when a liquid freezes?
1 Answer
The average kinetic energy stays constant overall (the lost energy is transformed into potential energy and released back into the system as heat, which becomes vibrational kinetic energy), even though the particles slow down.
However, their temperature and thus average kinetic energy does not change during the freezing.
(Molecular rotations essentially stop, and the molecules can't fly across the room, but the molecules vibrate more vigorously in place.)
Take for example a closed container of water where heat is extracted from it.
During any phase transition, the temperature is constant, because the two phases are in equilibrium with each other. As an added note, ordinary phase transitions are also at constant pressure.
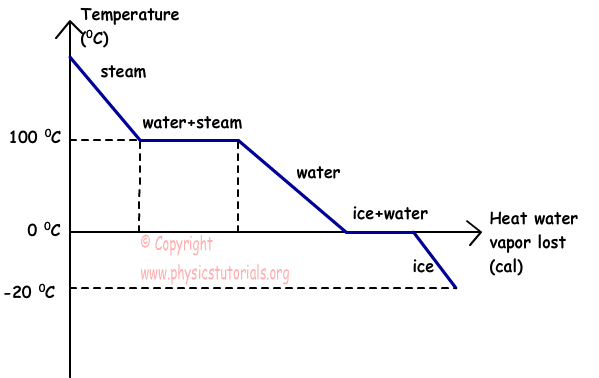
As water freezes, it does so because after thermal energy leaves the particles (freezing is exothermic), the average translational+rotational kinetic energy decreases, but the total average kinetic energy does not... and the temperature does not change either.
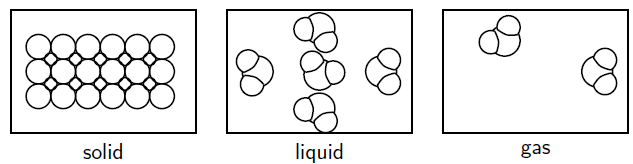
This is because for liquids and solids, which have considerably higher densities than gases (more closely-packed), the temperature of the water is not just dependent on the translational+rotational kinetic energy...
It's also dependent on the released potential energy from the stronger intermolecular forces that form, which becomes vibrational kinetic energy.
#T prop (overbrace(barK_(tr,rot))^"average non-vib kinetic energy" + overbrace(barK_(vib))^"average vib kinetic energy")#
So, the total average kinetic energy in the container of water remains the same, except redistributed into vibrational kinetic energy after the formation of ice.
#underbrace(overbrace(barK_(tr,rot))^"decreases")_"average non-vib kinetic energy" + underbrace(overbrace(barK_(vib))^"increases")_"average vib kinetic energy" = underbrace(overbrace(barK_(t ot))^"constant")_"total average kinetic energy"#
That keeps the temperature the same during the phase transition.

