Question #9f419
1 Answer
Here's what I got.
Explanation:
The magnetic quantum number,
Simply put, the magnetic quantum number tells you the exact orbital in which an electron is located inside an atom.
The value of the magnetic quantum number depends on the value of the angular momentum quantum number,
In turn, the magnetic quantum number depends on the value of the principal quantum number,
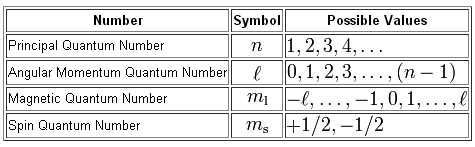
Now, an
#m_l = 0 -># represents an s orbital regardless of energy level
A
#m_l = (-1, 0 ,1 } -> # represent one of the three p orbitals regardless of energy level, as long as#n >1#
You can thus say that the
#p_x -> m_l = -1# #p_z -> m_l = 0# #p_y -> m_l = +1#

