Question #9f672
1 Answer
Here's what I got.
Explanation:
The thing to keep in mind here is that bismuth-203 undergoes beta positive decay, or positron emission, not beta minus decay, which more often than not is simply called beta decay.
https://en.wikipedia.org/wiki/Isotopes_of_bismuth
When a radioactive nuclide undergoes positron emission, a proton is converted to a neutron and a positron,
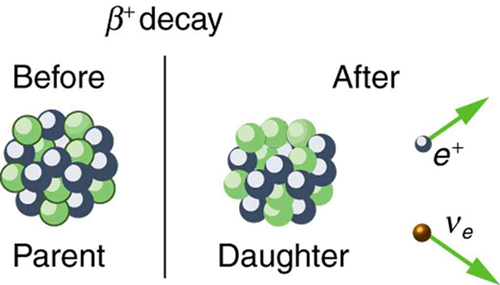
This means that--keep in mind that charge and mass are conserved in a nuclear reaction!
- the atomic number of the nuclide,
#Z# , will decrease by#1# - the mass number of the nuclide,
#A# , will remain unchanged
So, you can write
#""_ (color(white)(1)83)^203"Bi" -> ""_ Z^A"?" + ""_ 1^0"e" + nu_ "e"#
The atomic number decreases by
#83 = Z + 1 implies Z = 82#
The mass number remains unchanged, so
#203 = A + 0 implies A = 203#
Grab a Periodic Table and look for the element with the atomic number equal to
The balanced nuclear equation that describes the position emission of bismuth-203 will thus look like this
#""_ (color(white)(1)83)^203"Bi" -> ""_ (color(white)(1)82)^203"Pb" + ""_ 1^0"e" + nu_ "e"#

