What is the maximum number of electrons that can occupy the l = 4 subshell? What are the possible sets of 4 quantum numbers for an electron in n = 4 orbitals?
1 Answer
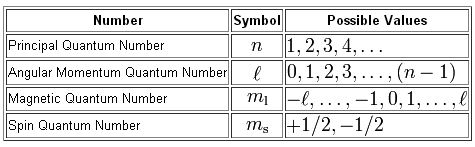
The angular momentum quantum number refers to the type of orbital and it can have multiple values for a single energy level.
Its value can be determined from magnetic quantum number and principal quantum number.
l = 0, 1, . . . , n-1
Therefore in this case the energy level can be
Qusetion 1 What is the maximum number of electrons that can occupy a given subshell of
Starting with the first problem
As

First you to need to know the number of orbitals in the g subshell. Knowing that the number of degenerate orbitals is
2l +1 = 2*4 + 1 = "9 orbitals" ,
and as each orbital can hold 2 electrons, electrons in 9 orbitals
= 9*2 = 18 e^-
Question 2 What are possible quantum numbers for an electron at energy level four?
The possible quantum numbers for
l = 0,1,2,3,
m_l " for " l = 3" = {-3,-2,-1,0,1,2,3}
m_l " for " l = 2" = {-2,-1,0,1,2}
m_l " for " l = 1" = {-1,0,1}
m_l " for " l = 0" = {0}


