Question #eef4c
1 Answer
Here's what I got.
Explanation:
For starters, you need a balanced chemical equation to go by.
#"N"_ (2(g)) + 3"H"_ (2(g)) -> 2"NH" _ (3(g))#
As you can see, nitrogen gas and hydrogen gas react in a
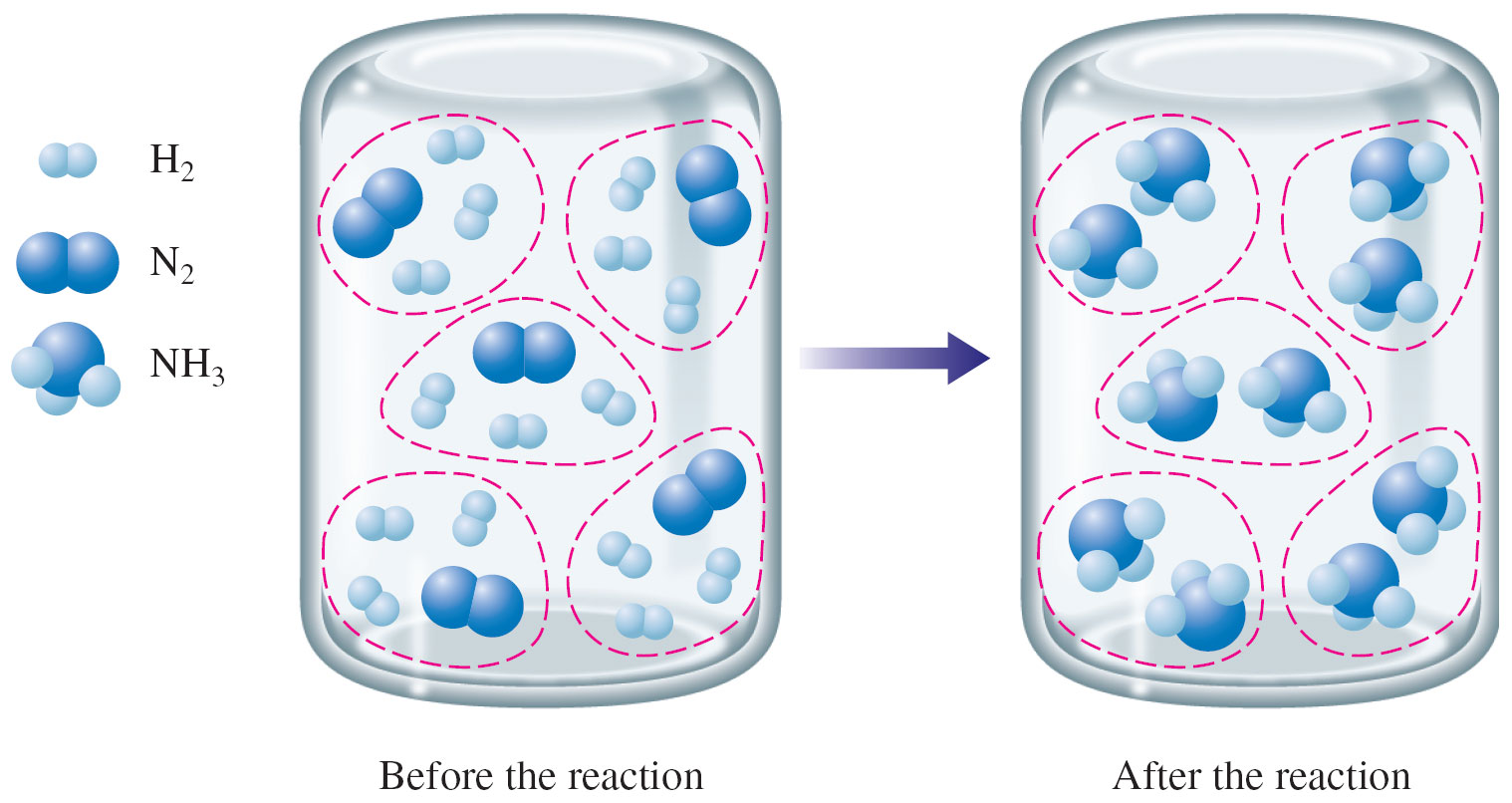
Now, use the molar masses of the two reactants to convert the masses to moles.
#20 color(red)(cancel(color(black)("g"))) * "1 mole N"_2/(28.0134color(red)(cancel(color(black)("g")))) = "0.7139 moles N"_2#
#13.5 color(red)(cancel(color(black)("g"))) * "1 mole H"_2/(2.0159 color(red)(cancel(color(black)("g")))) = "6.697 moles H"_2#
Notice that you have more hydrogen gas than you would need to ensure that all the moles of nitrogen gas react since
#0.7139 color(red)(cancel(color(black)("moles N"_2))) * "3 moles H"_2/(1color(red)(cancel(color(black)("mole N"_2)))) = "2.142 moles H"_2#
This means that hydrogen gas is in excess, which is equivalent to saying that nitrogen gas acts as a limiting reagent, i.e. it gets completely consumed by the reaction before all the moles of hydrogen gas can get the chance to react.
So, you can say that the reaction will consume
#0.7139 color(red)(cancel(color(black)("moles N"_2))) * "2 moles NH"_3/(1color(red)(cancel(color(black)("mole N"_2)))) = "1.428 moles NH"_3#
To convert this to grams, use the molar mass of ammonia.
#1.428 color(red)(cancel(color(black)("moles NH"_3))) * "17.0305 g"/(1color(red)(cancel(color(black)("mole NH"_3)))) = color(darkgreen)(ul(color(black)("24 g")))#
I'll leave the answer rounded to two sig figs, but keep in mind that it should be rounded to one significant figure, the number of sig figs you have for the mass of nitrogen gas.

