Question #f2414

1 Answer
Stefan V.
Jul 9, 2017

Grab a Periodic Table!

Explanation:

Your tool of choice here will be good old Periodic Table of Elements, so grab one and look for rubidium, #"Rb"#.

You should find this element in period #color(red)(5)# , group #color(blue)(1)#.

http://www.knowledgedoor.com/2/elements_handbook/rubidium.html

Now, you should know that the principal quantum number, #n#, which tells you the energy level on which an electron resides, also tells you the period in which the element that has this electron as its outermost electron is located.

In your case, rubidium is located in period #color(red)(5)#, so its outermost electron will have

#n = color(red)(5)#

You should also know that the Periodic Table is divided into blocks.

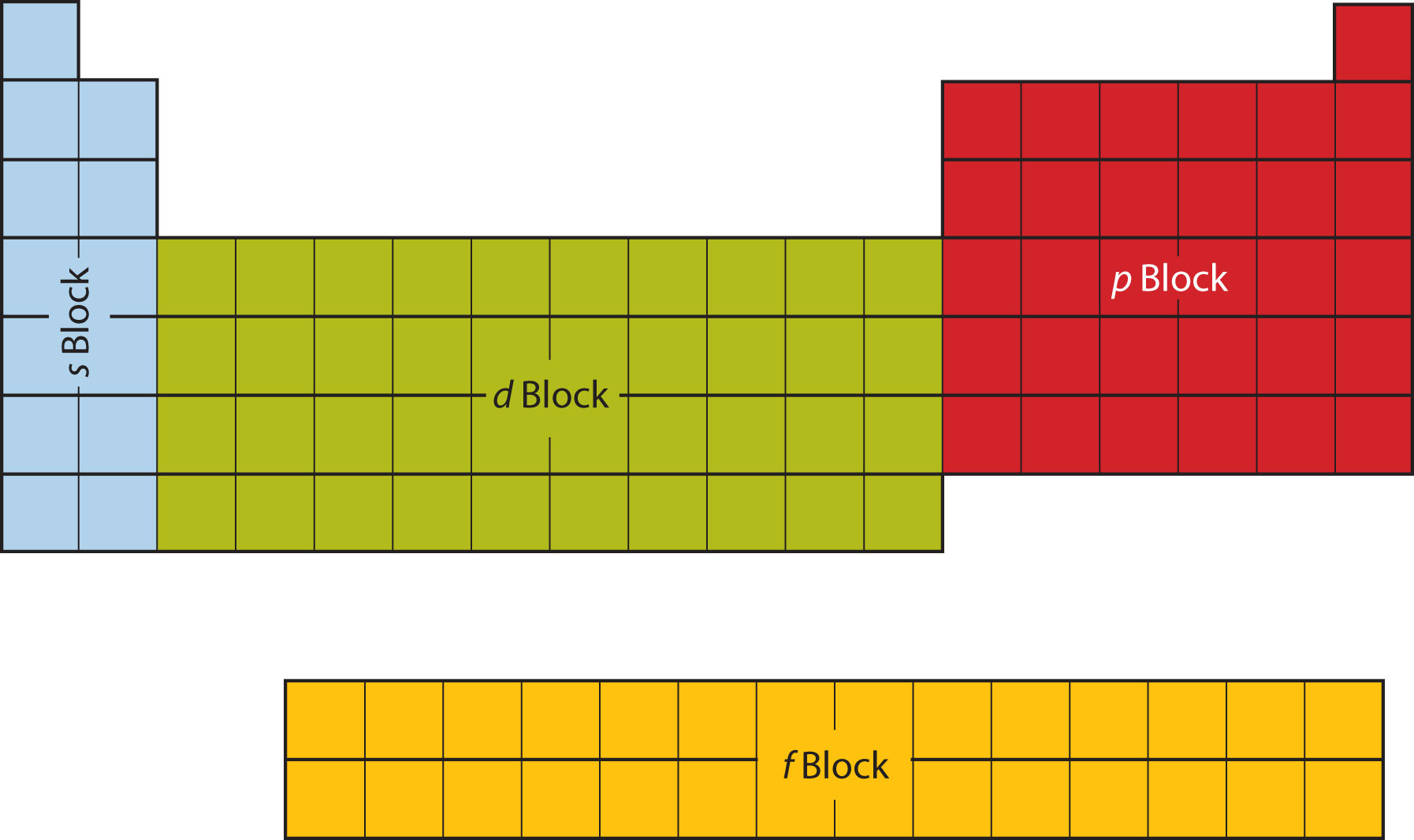
https://saylordotorg.github.io/text_introductory-chemistry/s12-04-electronic-structure-and-the-p.html

As you can see, the elements located in groups #1# and #2# make up the #s# block of the Periodic Table.

This means that their outermost electron(s) are located in the #s# subshell. The subshell in which an electron resides inside an atom is given by the angular momentum quantum number, #l#.

You will have

  • #l = 0 -># the #s# subshell
  • #l=1 -># the #p# subshell
  • #l = 2 -># the #d# subshell
  • #vdots#

and so on. In your case, rubidium is located in group #color(blue)(1)#, which means that it has

#l = color(blue)(0) -># the #s# subshell regardless of the value of #n#

You now have

#n = color(red)(5), l = color(blue)(0)#

The third quantum number in the set is the magnetic quantum number, #m_l#, which tells you the individual orbital that holds the electron.

Since the magnetic quantum number can only take one possible value for the #s# subshell

#l = 0 implies m_l = 0#

you can say that you now have

#n = color(red)(5), l = color(blue)(0), m_l = 0#

Finally, the spin quantum number, #m_s#, which tells you the spin of the electron, can only take two possible values

#m_s = {-1/2, +1/2}#

By convention, every electron that occupies an empty orbital, i.e. an electron that is present in an orbital by itself (an unpaired electron), is taken to have spin-up, which corresponds to

#m_2 = +1/2 -># an electron that has spin-up

This means that the full set of quantum numbers that describes the outermost electron of rubidium is

#n = 5, l =0, m_l = 0, m_s = +1/2#

Related questions
See all questions in Quantum Numbers
Impact of this question
6261 views around the world
You can reuse this answer
Creative Commons License