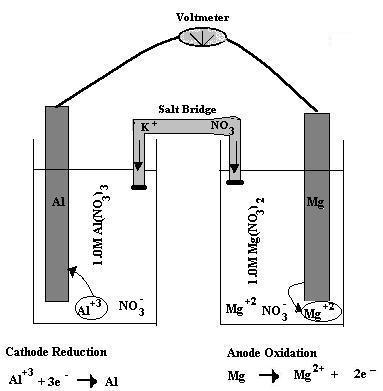
Question #8ab70
1 Answer
See below.
Explanation:
I'm not really sure what you need here because the problem actually tells you what you must do in order to get the answer right--balance the number of electrons!
So know that aluminium cations,
#"Al"^(3+) + 3"e"^(-) -> "Al"#
This takes place at the cathode.
Magnesium metal, on the other hand, is being oxidized to magnesium cations,
#"Mg" -> "Mg"^(2+) + 2"e"^(-)#
This takes place at the anode.
Now, in any redox reaction, the number of electrons lost in the oxidation half-reaction must be equal to the number of electrons gained in the reduction half-reaction.
In other words, all the electrons that are used to reduce a species must come exclusively from the species that is being oxidized.
So every atom of magnesium provides
#{("Al"^(3+) + 3"e"^(-) -> "Al" color(white)(aaaaaaaaaaa) | xx 2), (color(white)(aaaaaaa)"Mg" -> "Mg"^(2+) + 2"e"^(-) " " | xx 3) :}#
This means that you have
#{(2"Al"^(3+) + 6"e"^(-) -> 2"Al"), (color(white)(aaaaaaa)3"Mg" -> 3"Mg"^(2+) + 6"e"^(-)) :}#
#color(white)(aaaaaaaaaaaaaaaaaaaaaaaaaaa)/color(white)(a)#
#2"Al"^(3+) + color(red)(cancel(color(black)(6"e"^(-)))) + 3"Mg" -> 2"Al" + color(red)(cancel(color(black)(6"e"^(-)))) + 3"Mg"^(2+)#
which gets you
#2"Al"^(3+) + 3"Mg" -> 3"Mg"^(2+) + 2"Al"#
The galvanic cell would look something like this