A $20g$ mass of phosphoric acid dissolved in $250.0mL$ aqueous solution, reaches a stoichiometric end-point with WHAT volume of $NaOH(aq)$ at $0.120molL^-1$ concentration?

Question

1699 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-31T03:30:55

We need (i) a stoichiometric equation.....

$H_3PO_4(aq) + 2NaOH rarr Na_2HPO_4 +2H_2O(l)$

Note a stoichiometric endpoint is reached upon the addition of 2 equiv of base.

$"Concentration"$ $[H_3PO_4]="Moles of phosphoric acid"/"Volume of solution"$

$=((20.0*g)/(98.08*g*mol^-1))/(250*mLxx10^-3*L*mL^-1)=0.816*mol*L^-1$

And (ii) we need equivalent quantitites of $NaOH$ when $20*mL$ is tritrated.

$=(0.816*mol*L^-1xx20xx10^-3*L)/(1/2xx0.120*mol*L^-1)=0.272*L$

$=27.2*mL$ .

Phosphoric acid is a diacid in aqueous solution.

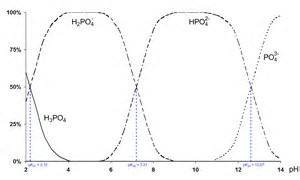commons.wikimedia.org

A 20*g20*g mass of phosphoric acid dissolved in 250.0*mL250.0*mL aqueous solution, reaches a stoichiometric end-point with WHAT volume of NaOH(aq)NaOH(aq) at 0.120*mol*L^-10.120*mol*L^-1 concentration?