Question

A sphere of diameter `12cm.` is cut by a plane dividing it in two parts. If surface area of the two parts are in the ratio `2:3`, find the distance of the plane from the center?

Answer 1

The plane should be passed at a distance of `2.4cm.` from the center.

Explanation:

Let us consider the sphere, cut by a plane at a distance of `h` from its surface as shown. The sphere has a diameter of `24cm.` i.e. radius of `12cm.`. However, we take it as `r` and then substitute `r=12`. Observe that domain of `h` is given by `0<=h<=2r`.

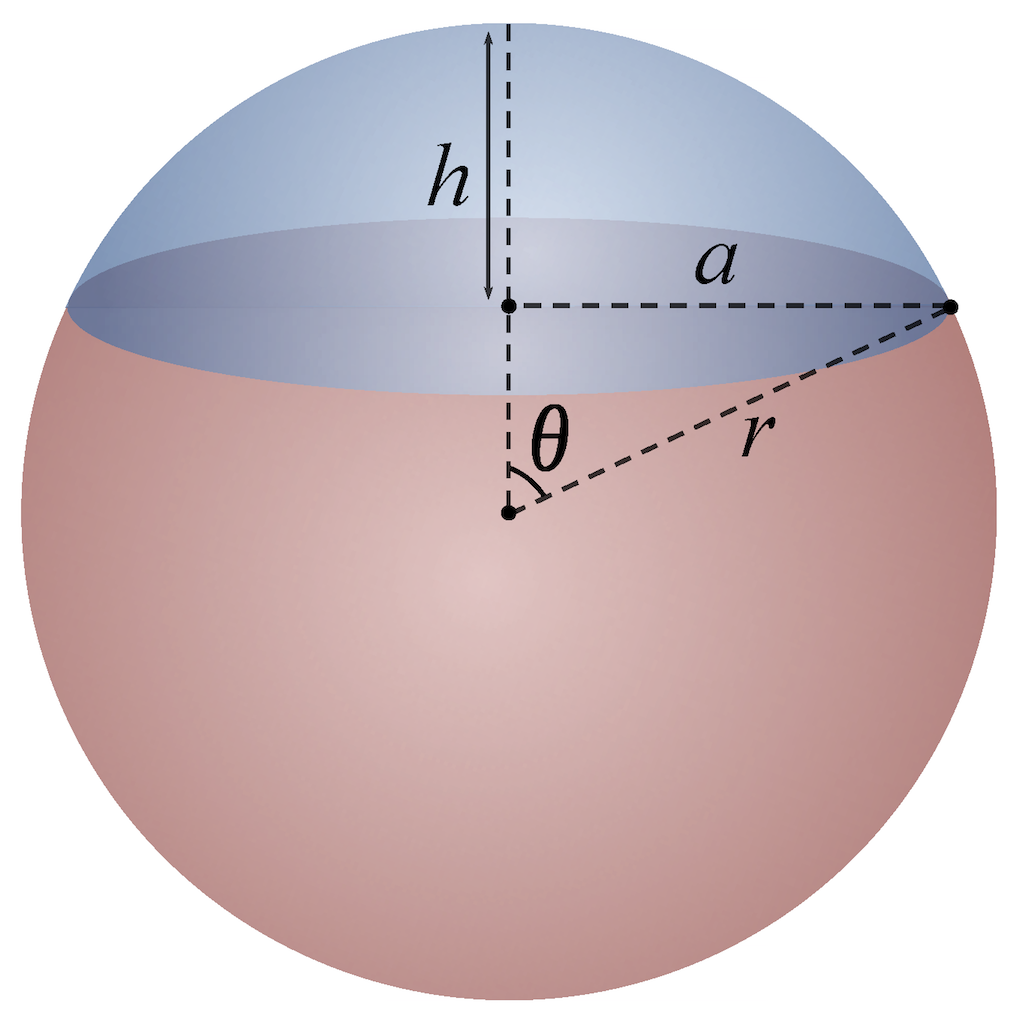
The plane cuts the sphere at a distance of `h` as shown. Formulas are available here It divides sphere in two parts, one the blue cap and the lower pink portion.

Surface area of the cap is given by formula `2pirh` and hence surface area of remaining sphere is `4pir^2-2pirh`. As they are in the ratio `2:3`, we have

`(2pirh)/(4pir^2-2pirh)=2/3`

or `h/(2r-h)=2/3`, where `r=12`

Hence, `3h=4xx12-2h`

or `5h=48`

i.e. `h=9.6cm.` or `12-9.6=2.4cm.` from center.

A detailed discussion on the topic is available here