At a certain temperature, is an equilibrium process endothermic or exothermic, if #K < 1#?
1 Answer
Endothermic, probably, as the energy of the products is higher than that of the reactants, for a given NONSTANDARD temperature (hence, at equilibrium,
Recall the Arrhenius equation and the definition of the equilibrium constant:
#k_(fwd) = Ae^(-E_(a,fwd)//RT)#
#k_(rev) = Ae^(-E_(a,rev)//RT)#
#K = k_(fwd)/(k_(rev))#
Since
(Note that
Something that isn't so obvious is that the change in entropy for a given reaction tends to be significantly smaller than the change in enthalpy or Gibbs' free energy.
Hence, people often use these two diagrams interchangeably (which isn't necessarily accurate, as it depends on the temperature):
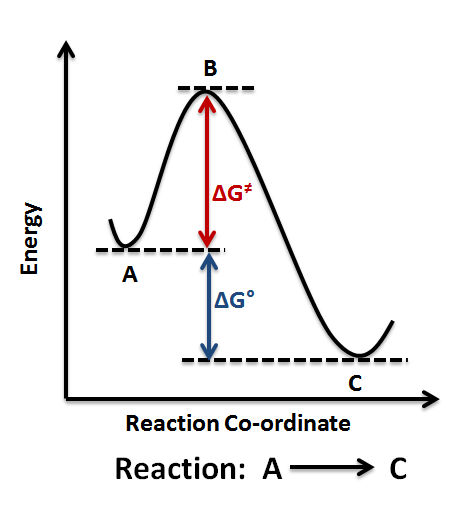
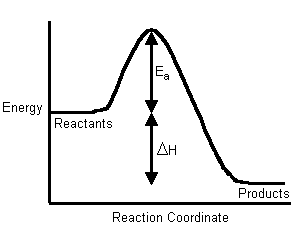
If the activation energy is larger for the forward reaction, our first inclination is to say the reaction is nonspontaneous, as the reverse reaction dominates due to its lower activation energy.
HOWEVER, since the reaction is at chemical equilibrium, we can actually clarify that the reaction is neither spontaneous nor nonspontaneous. The rates of the forward and reverse reactions are equal, i.e.
#cancel(DeltaG)^(0) = overbrace(DeltaG^@)^"not necessarily zero" + RTlncancel(Q)^(K)#
Instead, all we can say is that the reaction was endothermic, since the reactants must absorb energy in order to become products.

