Question

Question #1b269

Answer 1

Here's why that is the case.

Explanation:

Your quantum number set cannot describe an electron in an atom because the value of the magnetic quantum number, `m_l`, is not permitted given the value of the angular momentum quantum number, `l`.

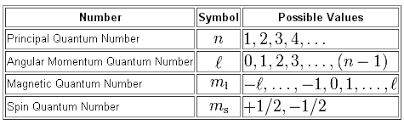
In your case, you have

`(color(red)(3), color(blue)(2), color(purple)(3), -1/2)`

The electron is said to be located on the third energy level, which has `n=color(red)(3)`, in the `d` subshell, which is denoted by

`l = color(blue)(2)`

For the `d` subshell, the magnetic quantum number is restricted to a total of `5` values

`m_l = {-2, -1, 0, 1, 2}`

As you can see, `m_l = color(purple)(3)` is not possible for an electron located in the `d` subshell `->` this quantum nubmer set cannot describe an electron in an atom.