Question

Question #51981

Answer 1

`n=3, l=1, m_l = -1, m_s = +1/2`

Explanation:

For starters, grab a Periodic Table and look for silicon, `"Si"`. You should find it in period 3, group 14.

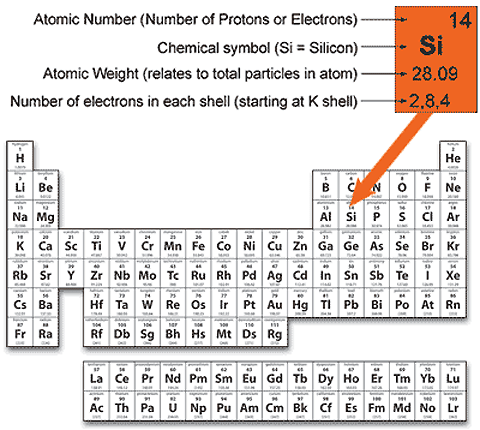
Now, notice that silicon has an atomic number equal to `14`. This means that a neutral silicon atom has `14` protons inside its nucleus and `14` electrons surrounding its nucleus.

In your case, you need to find the set of quantum numbers that describe the `"13th"` electron in a neutral silicon atom.

To do that, use the fact that the Periodic Table can be organized in blocks.

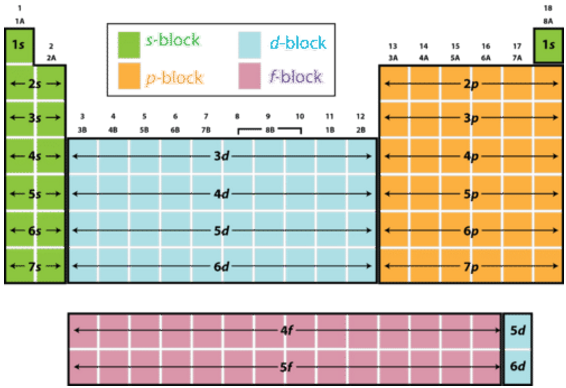
In your case, the last `2` electrons added to a neutral silicon atom are located in the `p` block.

This means that these electrons will have the angular momentum quantum number, `l`, equal to `1`.

`l = 1 ->` describes an electron located in the `p` block

The period in which silicon is located will give you the value of the principal quantum number, `n`. In your case, silicon is located in period `3`, so the principal quantum number will be equal to `3`.

`n = 3 ->` describes an electron located on the third energy level

Now, in order to find the magnetic quantum number, `m_l`, which gives you the orientation of the orbital in which the electron is located, you need to use the fact that the `p` subshell can hold a total of three `p` orbitals.

`l = 1 implies m_l = { (-1 -> "the p"_xcolor(white)(.)"orbital"), (color(white)(+)0 -> "the p"_zcolor(white)(.)"orbital"), (+1 -> "the p"_ycolor(white)(.)"orbital") :}`

In your case, the `"13th"` electron will be added to the first empty `3p` orbital, which, by convention, will have `m_l = -1`.

`m_l = -1 ->` describes and electron located in a `p_x` orbital

Finally, the spin quantum number, `m_s`, which tells you the spin of the electron, is equal to

`m_s = {( +1/2 -> "the electron is added to an empty orbital"), ( -1/2 -> "the electron is added to a half-filled orbital") :}`

Since the `"13th"` is added to the first empty `3p_x` orbital, you can say that you have

`m_s = +1/2 ->` describes and electron that has spin-up

Therefore, you can say that the quantum number set that describes the `"13th"` electron in a neutral silicon atom is

`n = 3, l= 1, m_l = -1, m_s = +1/2`

This electron is located on the third energy level, in the `3p` subshell, in the `3p_x` orbital, and has spin-up