What is the Fermi level? I heard it is also called the chemical potential.

1 Answer
Truong-Son N.
Dec 29, 2017

The Fermi level #epsilon_F# is otherwise known as the electron chemical potential (i.e. the molar Gibbs' free energy), since the chemical potential of the electrons is defined as the Fermi level at #"0 K"#, i.e. #mu = epsilon_F#.

For a semiconductor, it lies halfway between the bottom of the conduction band and the top of the valence band:

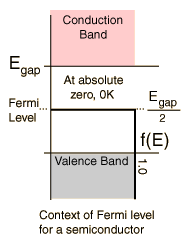
http://hyperphysics.phy-astr.gsu.edu/

A detailed derivation is shown here for the fundamental distribution law of Fermi-Dirac particles, among which are electrons.

From that derivation, we obtained the Fermi distribution function (for electrons only, not bosons):

#f(epsilon_i) = 1/(1 + e^((epsilon_i - epsilon_F)//k_BT))#

And for this, we have three cases of occupied electron energy states for arbitrary nonnegative temperatures. That is summarized here with an example at #"300 K"# (no units):

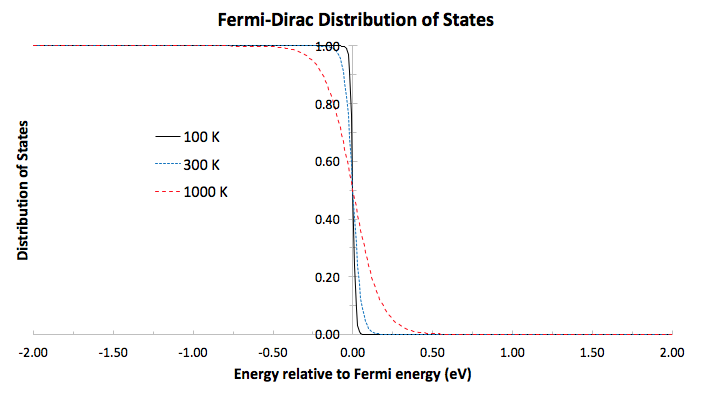
These cases are:

#bb(epsilon_i > epsilon_F)#

When this is the case, #0 < e^((epsilon_i - epsilon_F)//k_BT) < 1#, so
#0 < f(epsilon_i) < 1/2#.

#bb(epsilon_i = epsilon_F)#

When this is the case, #e^((epsilon_i - epsilon_F)//k_BT) = 1#, so
#f(epsilon_i) = 1/2# exactly.

#bb(epsilon_i < epsilon_F)#

When this is the case, #e^((epsilon_i - epsilon_F)//k_BT) > 1#, so
#1/2 < f(epsilon_i) < 1#.

For varying temperatures, we would see the following:

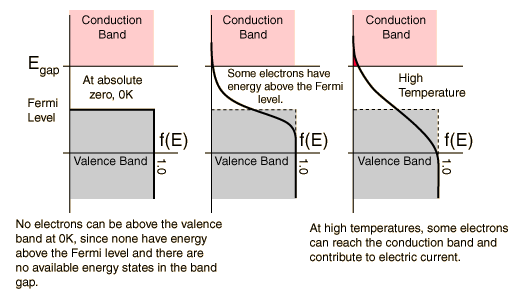
http://hyperphysics.phy-astr.gsu.edu/

And we would see that as #Tuarr#, the chemical potential of all the electrons near the Fermi level diverge, promoting conductivity, while at #"0 K"# exactly, there is a rigid cutoff at the Fermi level.

Put another way, at very low temperature, conductivity is limited because little electron density can surpass the Fermi level.

EXAMPLE

Now, consider that we are at #"298.15 K"# (#25^@ "C"#). Suppose we wanted to see the fraction of electrons that occupy states #"0.36 eV"# above the Fermi level, as would be the minimum case for conductivity in germanium atom.

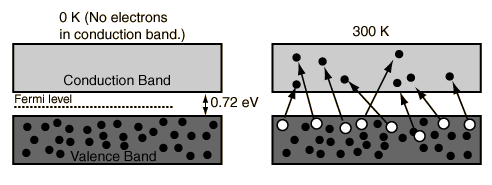
http://hyperphysics.phy-astr.gsu.edu/

Then:

#f(epsilon_F + "0.36 eV") = 1/(1 + e^((epsilon_F + "0.36 eV" - epsilon_F)//k_BT))#

#= 1/(1 + e^("0.36 eV"//k_BT))#

The Boltzmann factor is

#k_BT = 1.38065 xx 10^(-23) cancel"J""/"cancel"K" xx 298.15 cancel"K" xx ("1 eV")/(1.602 xx 10^(-19) cancel"J")#

#=# #"0.02570 eV"#

So the fraction of electron states occupied #"0.36 eV"# above the Fermi level at #"298.15 K"# is:

#color(blue)(f(epsilon_F + "0.36 eV")) = 1/(1 + e^("0.36 eV"//"0.02570 eV"))#

#= color(blue)(8.23 xx 10^(-7))#

Related questions
Impact of this question
8013 views around the world
You can reuse this answer
Creative Commons License