Question

Question #a51c8

Answer 1

The point `(1,4)` has a horizontal tangent line.
The point `(0,5)` has a vertical tangent line.

Explanation:

Firstly, here are the steps for the differentiation.

Differentiate everything (implicitly) with respect to `x`.

`2x - 2 (y + x frac{dy}{dx}) + 2y frac{dy}{dx} + 6 - 10 frac{dy}{dx} = 0`

Bring all the terms containing `frac{dy}{dx}` to one side of the equation.

`2x - 2y + 6 = 2x frac{dy}{dx} - 2y frac{dy}{dx} + 10 frac{dy}{dx}`

Remove the common multiple of 2.

`x - y + 3 = x frac{dy}{dx} - y frac{dy}{dx} + 5 frac{dy}{dx}`

Make `frac{dy}{dx}` the subject of formula.

`frac{dy}{dx} = frac{ x - y + 3 }{x - y + 5}`

Which is what you have gotten.

To find the point(s) with horizontal tangent line, you should look for points `(x,y)` such that `frac{dy}{dx}` is zero.

`frac{dy}{dx} = frac{ x - y + 3 }{x - y + 5} = 0`

which simplifies to

`y = x + 3`

Bear in mind that the point `(x,y)` also has to satisfy the condition of lying on the parabola.

`x^2 - 2xy + y^2 + 6x - 10y + 25 = 0`

Solve this simultaneous equation by substitution.

`x^2 - 2x(x + 3) + (x + 3)^2 + 6x - 10(x + 3) + 25 = 0`

Expanding the terms reveal that the `x` squared terms cancel out.

`4 - 4x = 0`

`x = 1`

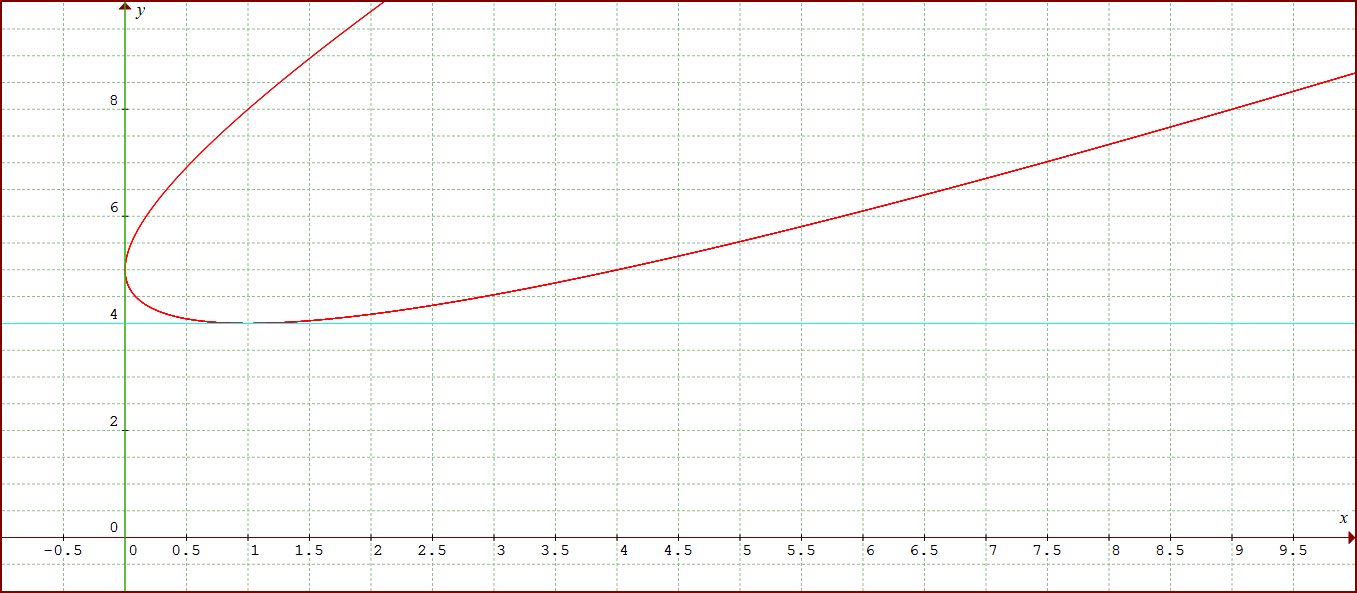
`y = 1 + 3 = 4`

The point `(1,4)` has a horizontal tangent line. The equation of the tangent line is `y = 4`.

To find the point(s) with vertical tangent line, you should look for points `(x,y)` such that `frac{dy}{dx}` does not exist.

This is due to denominator being zero for a certain point `(x,y)`.

`x - y + 5 = 0`

or

`y = x + 5`

Again, the point `(x,y)` must lie on the parabola.

`x^2 - 2xy + y^2 + 6x - 10y + 25 = 0`

Substituting directly, we get the equation below.

`x^2 - 2x(x + 5) + (x + 5)^2 + 6x - 10(x + 5) + 25 = 0`

After expansion, we have a first order polynomial again.

`-4x = 0`

`x = 0`

`y = 5`

The point `(0,5)` has a vertical tangent line. The equation of the tangent line is `x = 0`.

Refer to the graph below. The horizontal tangent is in cyan while the vertical tangent is in lime.