Question

The base of a prism is in the shape of a rhombus, whose diagonals and height of the prism is given. How do we find its volume?

Answer 1

Volume of pyramid with rhombus base `=(1/2)d_1d_2h`

Explanation:

Volume of pyramid is `(1/3)*` base area * height).
This formula remains same for all pyramids.

For a cone, it is `(1/3)*pir^2*h` where `pir^2` is base area and h is the height.

Likewise, area of a pyramid with rhombus base is
= (Base area * height).
Area of Rhombus is given by `((1/2)* d_1 * d_2)` where `d_1 and d_2` are the diagonals of the rhombus.

`:.` volume of pyramid with rhombus base = `(1/2)d_1d_2h`

Answer 2

Volume of a prism with rhombus base is `1/2abh`, where `a` and `b` are diagonals of the rhombus and `h` is the height of prism.

Explanation:

Volume of any prism is area of its base multiplied by its height.

As base is rhombus in shape and its area is half the product of its diagonals, if its diagonals are `a` and `b`, its area is `1/2ab`.

Hence, if height of a prism with rhombus base is `h`, its volume would be `1/2abh`.

Hence, volume of a prism with rhombus base is `1/2abh`, where `a` and `b` are diagonals of the rhombus and `h` is the height of prism.

Answer 3

See the example.

Explanation:

In general, the volume of a prism can be calculated by the formula
`V=Sh` , where `S` stands for the area of the base and `h` for the height.

Then, you have to calculate the area of the rhombus.
If the lengths of two diagonals in a rhombus are `a` and `b`, the area is `1/2ab`.

[Example1] Find the area of the rhombus below.

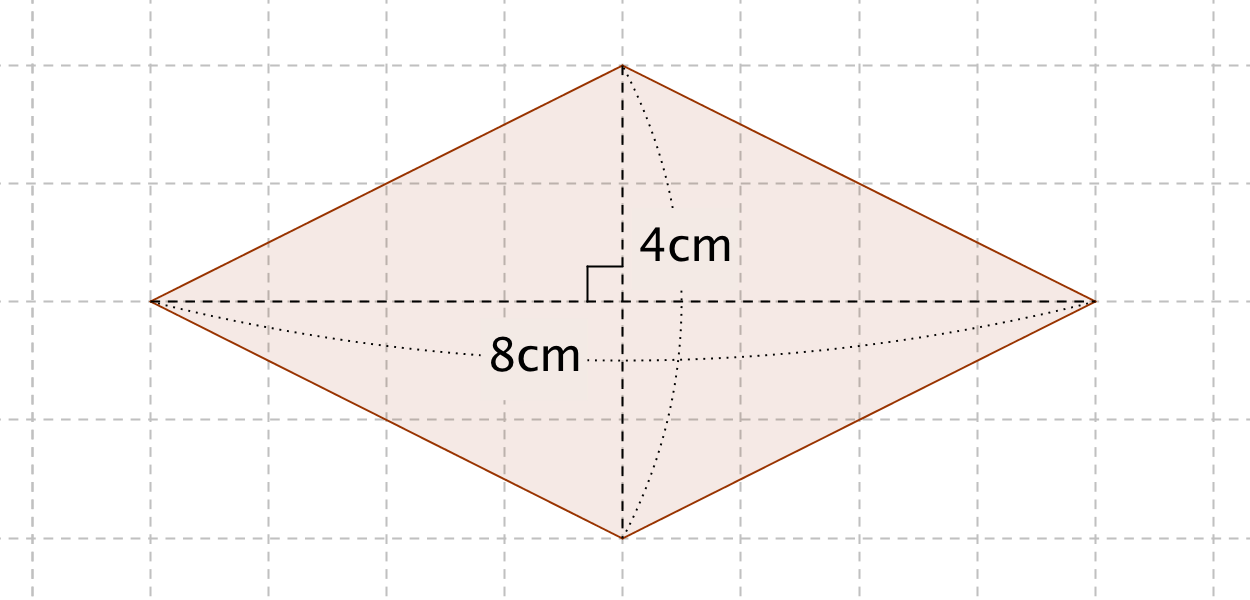
The lengths of the two diagonals are `4` cm and `8` cm.
Its area is `1/2*4*8=16` cm`"^2`.

[Example2] Evaluate the volume of a prism which has a base same as [Example1] and height `10` cm.

Area of base is `S=16` cm`""^2` and height is `h=10` cm.
Therefore, the volume is `V=Sh=16*10=160` cm`""^3`.