Question

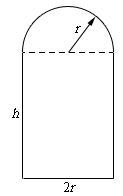
An arched window (an upper semi-circle and lower rectangle) has a total perimeter of `10 \ m`. What is the maximum area of the window?

Answer 1

The maximum area is `50/(4 + pi) (~~ 7.001)`. This occurs when:

radius of the semicircle is `10/(4 + pi)`
rectangular window is `10/(4+pi) xx 10/(4 + pi) (~~ 1.400 xx 1.400)`

Explanation:

Let us setup the following variables:

# { (r, "Radius of the semicircle","(m)"), (h=L, "Height of the rectangular window","(m)"), (A, "Total area enclosed by the window", "(sq m)") :} #

Our aim is to find `A(h,r)`, as a function of a single variable and to maximize the total area, `A`, wrt that variable (It won't matter which variable we do this with as we will get the same result). ie we want a critical point of `A` wrt the variable.

The total perimeter is that of `3` sides of the rectangle and the semicircle; we are told that this perimeter is `10` m

`10 = (h + 2r + h) + (1/2)(2pir)`
`\ \ \ = 2r + 2h + pi r`

`:. 2h = 10 - 2r - pi r`
`:. \ \ h = 1/2(10 - 2r - pi r)`

And the total Area is that of a rectangle and a semicircle:

`A = (h)(2r) + (1/2)(pir^2)`
`\ \ \ = 2hr + 1/2 pi r^2`
`\ \ \ = 2(1/2(10 - 2r - pi r))r + 1/2 pi r^2`
`\ \ \ = 10r - 2r^2 - pi r^2 + 1/2 pi r^2`
`\ \ \ = 10r - 2r^2 - 1/2 pi r^2`

We now have the Area, `A`, as a function of a single variable `r`, so differentiating wrt `x` we get:

`(dA)/(dr) = 10 - 4r - pi r`

At a critical point we have `(dA)/(dr) =0 =>`

`10 - 4r - pi r = 0`
`:. \ \ \ \ 4r + pi r = 10`
`:. \ \ \ r(4 + pi) = 10`
`:. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \r = 10/(4 + pi) (~~ 1.400)`

With this value of `r` we have:

`A = 10(10/(4 + pi)) - 2(10/(4 + pi))^2 - 1/2 pi (10/(4 + pi))^2`
`\ \ \ = 50/(4 + pi) (~~ 7.001)`

And:

`h = 1/2(10 - 2(10/(4 + pi)) - pi (10/(4 + pi)))`
`\ \ = 10/(4+pi) (~~ 1.400)`

We can visually verify that this corresponds to a maximum by looking at the graph of `y=A(r)`:

graph{10x - 2x^2 - 1/2 pi x^2 [-5, 10, -5, 22]}

And also check that the perimeter is correct:

`P = 2r + 2h + pi r`
`\ \ = 2(10/(4 + pi)) + 2(10/(4 + pi)) + pi(10/(4 + pi))`
`\ \ = 10`