.
intdx/sqrt(e^(2x)-1)
We will solve this by Trigonometric Substitution:
In the right triangle below:
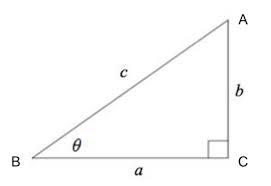
If c=e^x and a=1 we can use the Pythagoras' formula to solve for the length of side b
c^2=a^2+b^2
b^2=c^2-a^2
b=sqrt(c^2-a^2)=sqrt(e^(2x)-1
sectheta=c/a=e^x
tantheta=b/a=sqrt(e^(2x)-1
secthetatanthetad(theta)=e^xdx
dx=(secthetatanthetad(theta))/e^x=(secthetatanthetad(theta))/sectheta=tanthetad(theta)
We have all the pieces to substitute:
intdx/sqrt(e^(2x)-1)=int(1/sqrt(e^(2x)-1))(dx)=int1/tantheta*tanthetad(theta)=intd(theta)=theta+C
Now we can substitute back:
From tantheta=sqrt(e^(2x)-1 we have:
theta=arctansqrt(e^(2x)-1
Therefore:
intdx/sqrt(e^(2x)-1)=arctansqrt(e^(2x)-1)+C



