Question #8d970
1 Answer
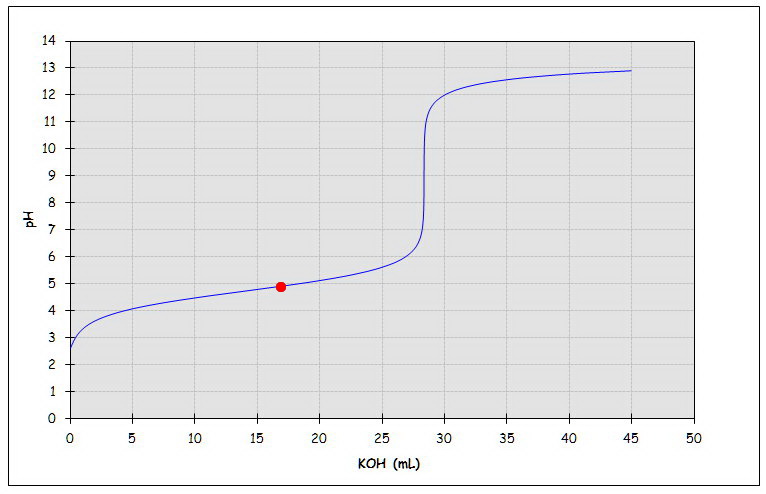
Warning! Long Answer. pH = 4.92
Explanation:
This type of problem involves two major steps:
First, figure out what is happening during the reaction and what you have in the solution at the end of the reaction.
Second, calculate the pH of that solution.
Step 1. What's happening?
The base is reacting with the acid and forming a salt.
This is a stoichiometry problem, so we must use moles in our calculations.
I usually set up an ICE table to organize my calculations.
The strong base will react completely with the acid.
Now, we put these numbers into the ICE table.
This tells us that we have a solution containing
What's a solution of a weak acid and its conjugate base? A Buffer!!!
Now we move to Step 2.
Step 2. Calculate the pH of the buffer
We have the equilibrium
We use the Henderson-Hasselbalch equation:
So,
Did you notice that I used moles instead of molarities in the above calculation?
I can do that because, if the two substances are in the same solution,
If you were plotting the titration curve, you would be at the position of the red dot in the graph.