Find the derivative using first principles? : #3x^2-4x #
1 Answer
# f'(x) = 6x-4 #
The coordinates we seek are
Explanation:
We have:
# f(x)=3x^2-4x #
Using the limit definition of the derivative, we can compute the derivative as follows:
# f'(x) = lim_(h rarr 0) ( f(x+h)-f(x) ) / h #
# \ \ \ \ \ \ \ \ = lim_(h rarr 0) ( (3(x+h)^2-4(x+h)) - (3x^2-4x) ) / h #
# \ \ \ \ \ \ \ \ = lim_(h rarr 0) ( (3(x^2+2xh+h^2)-4x-4h) - (3x^2-4x) ) / h #
# \ \ \ \ \ \ \ \ = lim_(h rarr 0) ( 3x^2+6xh+3h^2-4x-4h - 3x^2+4x ) / h #
# \ \ \ \ \ \ \ \ = lim_(h rarr 0) ( 6xh+3h^2-4h ) / h #
# \ \ \ \ \ \ \ \ = lim_(h rarr 0) ( 6x+3h-4 ) #
# \ \ \ \ \ \ \ \ = 6x-4 #
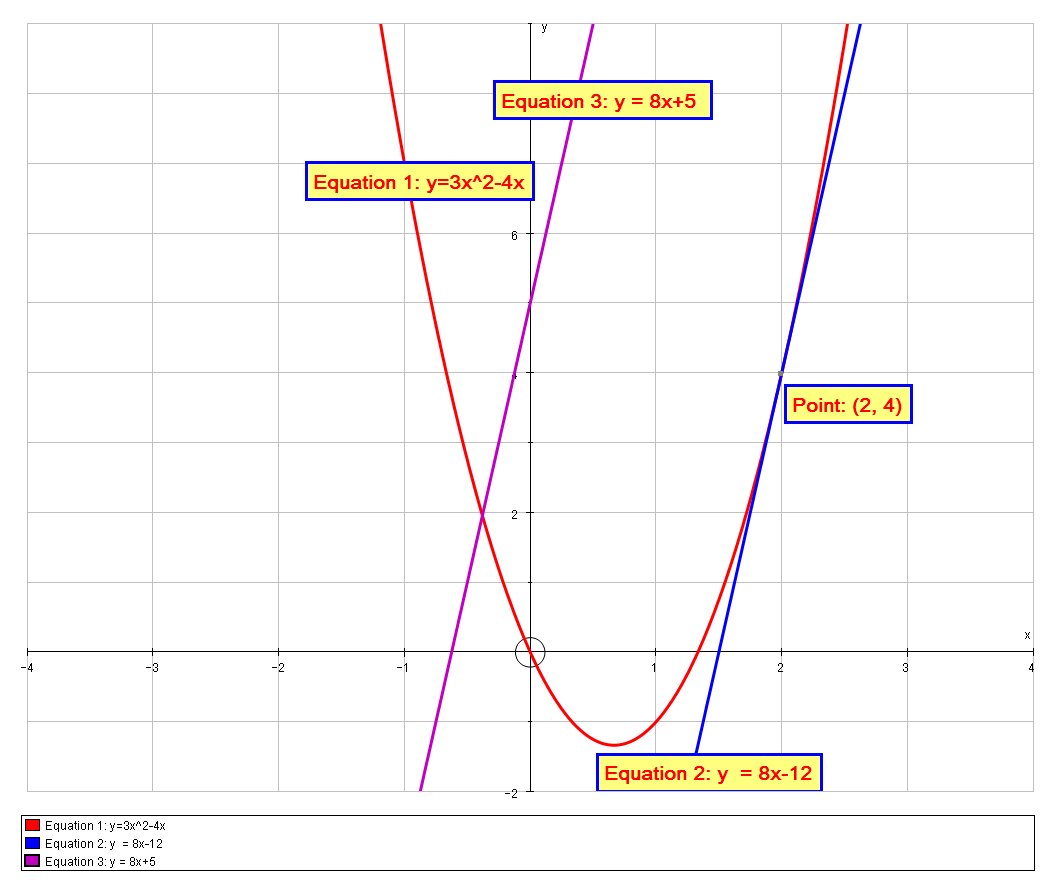
For the secondary part of the question we have a line with equation:
# y = 8x+5 #
Comparing with the standard form of a straight line ,
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is
# f'(x)= 8 => 6x-4=8 => x=2#
With
# f(2) = 3*4-4*2 = 4 #
So the tangent passes through the coordinate
Note tat should we require it, then using the point/slope form
# y -4 = 8(x-2) #
# :. y -4 = 8x-16 #
# :. y = 8x-12 #
And we can confirm this graphically: