Question

Question #4f1f4

Answer 1

Charles' Law.

Explanation:

Charles' Law states that when the pressure and the number of moles of gas present in a sample are kept constant, the volume of the gas and its temperature have a direct relationship.

This means that under these conditions, if you increase the temperature of the gas, its volume will increase as well. Similarly, if you decrease the temperature of the gas, its volume will decrease as well.

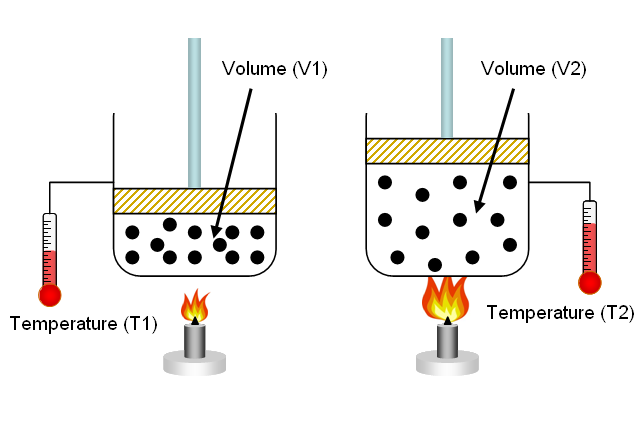
So, if you take `V_1` and `T_1` to be the volume and the temperature of the gas at an initial state and `V_2` and `T_2` to be the volume and temperature of the gas at a final state, you can say that

`V_1/T_1 = V_2/T_2 ->` Charles' Law

Keep in mind that this equation uses the temperature of the gas expressed in Kelvin!

So, for example, you can rearrange the equation to see how a change in temperature would affect the volume of the gas.

`V_2 = T_2/T_1 * V_1`

Notice that if the temperature of the gas increases

`T_2 > T_1`

then its volume will increase as well because

`V_2 = overbrace(T_2/T_1)^(color(blue)(>1)) * V_1 implies V_2 > V_1`

This is the case because when you increase the temperature of a gas, you increase the kinetic energy of its molecules. When that happens, the force and frequency with which these molecules hit the walls of the container increase.

When the pressure is kept constant, this increase in how hard and frequent the molecules hit the walls of the container causes the volume of the container to expand.