We have #f(x) = -3x#, to be vertically stretched by #4# units, and finally translated #4# units to the right, to get #g(x)#.
Firstly, it asks to be vertically stretched. What does it mean to be vertically stretched? It means that if you have any two points on the function, a constant vertically stretching the function will also multiply the vertical distance between those two points.
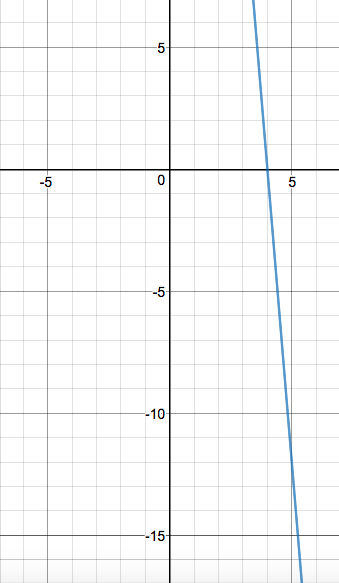
Here's what #f(x) = -3x# looks like when graphed:
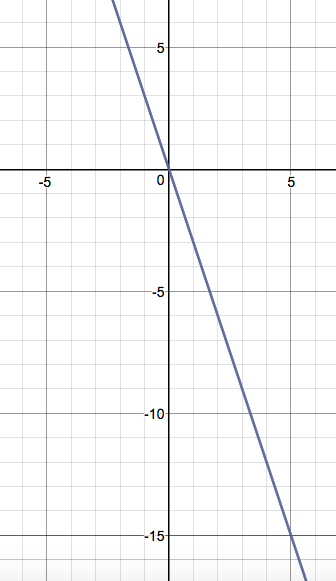
Let's say we have points A #(0, 0)# and B #(1, -3)# on the graph:
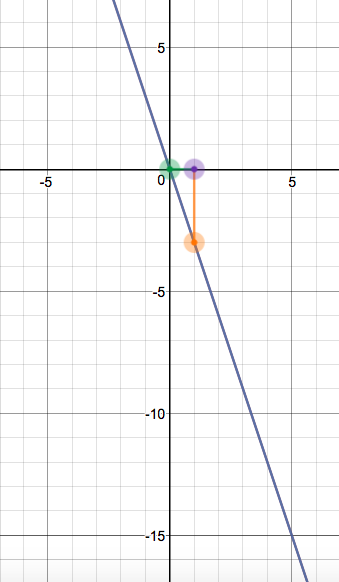
I've added an extra point C, taking the #x#-coordinate of B and the #y#-coordinate of A, which is in this case #(1, 0)#.
Together, all #3# points form a triangle, which can be used to calculate the slope (length of the strip between point B and point C divided by length of the strip between point A and point C; negatives indicate downwards direction), #-3#, as can also be seen in the equation for the function, #f(x) = -3x#.
Using that triangle, to strecth the line, we'd just need to make point B four times further from point A or point C, vertically. This can be done by multiplying the slope, which should change the length of that strip between point B and point C, don't you think?
#"Slope" = ("Strip between B and C")/("Strip between A and C")#
#m * Slope = (m * "Strip between B and C")/("Strip between A and C")#
Multiplying the slope, also multiplies the entire function:
#4 f(x) = 4 * -3x = -12x#
Let's see how that affects the line...
I've left the trail of the original line. #4f(x)# seems to be waaay steeper than #f(x)#, and the line has therefore been streched! By a factor of #4#, that is.
Now we just need to translate it #4# units to the right. A nice trick to do that is to decrease the input.
Why decrease, you may ask? By doing so, the input remains, but the output taken is as if the input is some amount less, so the new output is taken from the decreased input and used for the actual input, giving the impression of moving the point to the right. Do this for all points and the entire graph is translated.
To be honest, I think this is quite difficult to explain, but an example should help:
Say we have point B #(1, -3)#, which we want to translate by #4# units to the right to obtain B'. What would the coordinates be? Well, we would take the coordinates of point B, add #4# units to it, and - this is the important part - leave the #y#-value unchanged. That gets us #(5, -3)#.
Supposedly, when we plug in a value of #1# for #f(x) = -3x#, we would get #-3# for a #y#-value. This time, however, for an #x#-value of #5#, we want a #y#-value of #-3#.
But that #y#-value of #-3# is already assigned for an #x#-value of #1#, which is four units less.
So essentially, by having #-3(x - 4)#, we're saying, "OK, plug in the values of #x# as usual, but when evaluating, make sure to take the #y#-values that are #4# units behind."
Combining the streching and translating, we get:
#g(x) = -12(x - 4) = -12x + 48#
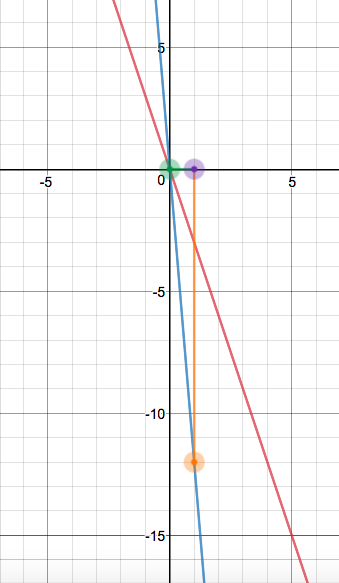
Here's the plot of #g(x)#, the blue strip, compared to #f(x)#, the red strip:
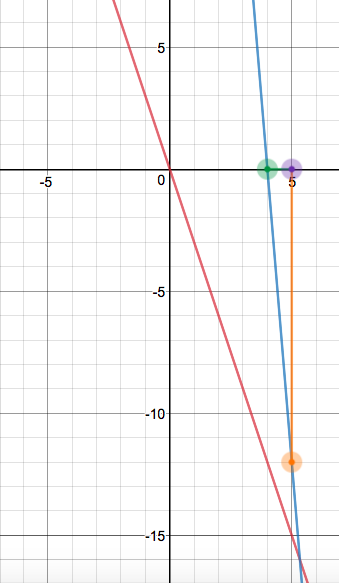
Here's #g(x)# alone: