Question

Given that `G(x)=-(x-4)^2+2`, determine the vertex ?

Answer 1

The vertex is `(4,2)`.

Explanation:

The general form `y = a*(x-h)^2 +k` of a quadratic has vertex `(h,k)`. It's really important to remember that there's a negative sign in front of `h` in the general form.

From your given function, `g(x) = -(x-4)^2 +2` we can see that the vertex is `(4,2)`.

Answer 2

Vertex`->(x,y)=(4,2)`

Explanation:

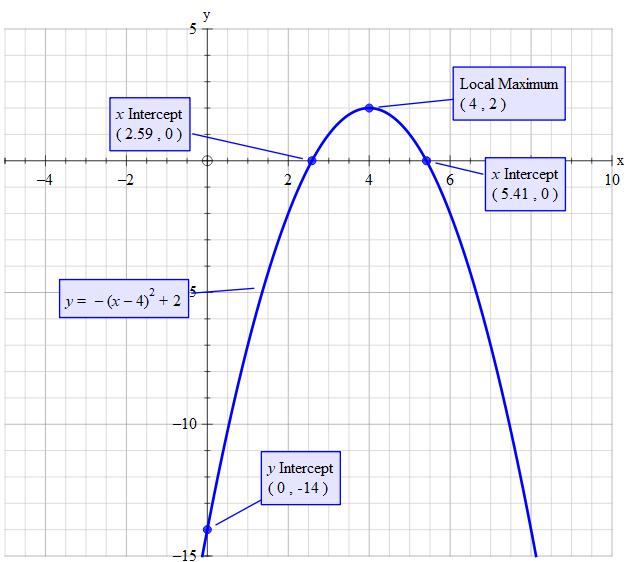
If you were to multiply out the brackets you would have the `x^2` term as: `-x^2`. As this is negative the graph is of shape `nn`. Thus the vertex is a maximum.

The format of `G(x)` is what they call completing the square. Sometimes referred to as the Vertex Form. You can ( with a little adjustment) read off directly the coordinates of the vertex.

Set `y=-(xcolor(red)(-4))^2 color(purple)(+2)`

`y_("vertex")= color(purple)(+2)`

`x_("vertex")=(-1)xxcolor(red)(-4) = +4" "larrul("Always")" multiply by (-1)"`

Thus we have:

Vertex`->(x,y)=(4,2)`