Question

Question #494b1

Answer 1

`64cm^3`

Explanation:

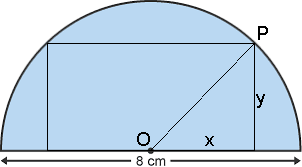
Consider the x and y coordinates of the triangle in the first quadrant of the semi circle. The length of the required rectangle will be `2x` and the height would be `y`. [since x is measured form the centre of the circle]

So the area of the rectangle required would be `2xy`, but this area is in terms of two variables and we require it as a function of one variable for differentiation.

We know from trig and the equation of a circle that `y=rsin theta` and`x=rcos theta`. where theta is the angle made between the x axis and the radius line.

Since the radius is `8` we have `x=8costheta...........[1] and y=8sintheta............[2]` and so the area, a, of the rectangle in terms of theta is `2[8costheta8sintheta]`=`128costhetasintheta`

Let a =area, and now differentiate a with respect to theta using the product rule. `d[uv]=vdu +udv`

`da`/d`theta`= `128cos^2theta-128sin^2theta`,

`128cos^2theta=128sin^2theta` and dividing both sides by `128cos^2theta` we get
`Sin^2theta /cos^2theta =1`, [so `tan^2theta =1]`, since `tantheta` =`sin theta /costheta`.

Remember `tan^2theta =[tantheta]^2`, so by taking the square root of both sides.`tan theta =1or -1`, but tangent is always positive in the first quadrant. `tan^_1[1]=45 degrees.`
,
so the area of the rectangle is `2xy`=`2[8cos45][8sin45]`=`128.sqrt2/2.sqrt2/2`=64. Since the angle is `45` degrees, `sin 45 =cos 45` so `x` must equal `y` and can be found by substituting this angle in `[1]`and `[2]` above . Also since `x=y` we can say `2x^2`=`8^2` so `x=y=sqrt32`.

One could also take the second derivative to see if it is negative but is not needed here, I believe,............[it is]. Hope this helps.

Answer 2

`"Area " = 64 \ cm^2`

Explanation:

We consider a rectangle inscribed in a semicircle of radius `8 \ cm`, as shown in the diagram:

Let us set up the following variables:

# { (x,"semi-width of the rectangle", cm), (y, "height of the rectangle ", cm), (A, "Area of the rectangle ", cm^2) :} #

Our aim is to find an area function, `A(x,y)` and eliminate one of the variables so that we can find the critical points wrt to the remaining variable.

The Area of the rectangle is given by:

`A = "width" xx "height"`
`\ \ \ = (2x)(y)`
`\ \ \ = 2xy` ..... [A}

Using Pythagoras we have:

`OP^2 = x^2 + y^2`
`:. 8^2 = x^2 + y^2`
`:. y^2 = 64 - x^2`

We could substitute for `y` in [A] by writing `y=sqrt(8^2 - x^2)`, and substituting into [A] to get:

`A = 2xsqrt(64 - x^2)` ..... [B]

However, we can get a cleaner solution by considering `A^2`, so from [A] we have:

`A^2 = 4x^2y^2`
`\ \ \ \ = 4x^2(64 - x^2)`
`\ \ \ \ = 256x^2-4x^4`

Differentiating (Implicitly) wrt `x` we get:

`2A (dA)/dx = 512x-16x^3`

At a critical point (a minimum or a maximum) we require that the derivative, `(dA)/dx` vanish, thus we require:

`2A xx 0 = 512x-16x^3`
`:. 512x-16x^3 = 0`
`:. 16x(32-x^2) = 0`
`:. 32-x^2 = 0`
`:. x^2 = 32`
`:. x=+- 4 sqrt(2)`

Obviously we require that `x gt 0`, so we discard the negative solution leaving us with `x=4sqrt(2)`

And, with this value of `x` we find that

`A^2= 4x^2(64 - x^2)`
`\ \ \ \ = 4(32)(64-32)`
`\ \ \ \ = 4(32)(32)`
`\ \ \ \ = 2^2 \ (32^2)`

And so,

`A = (2)(32)=64 \ cm^2`

We need to establish that this value of `x` corresponds to a maximum. This should be intuitive, but we can validate via a graph of the result [B] (or we could perform the second derivative test):
graph{2xsqrt(64 - x^2) [-2, 10, -5, 70]}

And we can verify that a maximum when `x=4sqrt(2) ~~ 5.7` of `64` is consistent with the graph.

Answer 3

`64 cm^2`

Explanation:

In addition to the great answers already posted, here is another attempt for a simpler solution. Consider the figure drawn below, depicting a rectangle ABCD drawn in a semicircle of radius 8cm,with its centre O

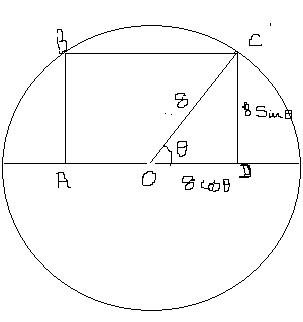
Length Ad of the rectangle would be `16 cos theta` and width CD would be `8 sin theta`

Area of rectangle would be `16 cos theta * 8 sin theta= 128 sin theta cos theta = 64 sin 2theta`

This would be maximum when `sin 2 theta`=1. which implies `2theta = pi/2`

This gives `theta = pi/4`

The maximum area would thus be `64 cm^2` with length of the rectangle being `16 cos theta= 8 sqrt2` and width `8sin theta= 4 sqrt2`