a) 0 mL
#color(white)(mmmmmmml)"HA" + "H"_2"O" ⇌ "A"^"-" + "H"_3"O"^"+"#
#"I/mol·L"^"-1":color(white)(mm)0.150color(white)(mmmmml)0color(white)(mmm)0#
#"C/mol·L"^"-1":color(white)(mmll)"-"xcolor(white)(mmmmml)"+"xcolor(white)(mm)"+"x#
#"E/mol·L"^"-1":color(white)(l)0.150 - xcolor(white)(mmmmll)xcolor(white)(mmm)x#
#K_"a" = (["H"_3"O"^+]["A"^"-"])/(["HA"]) = x^2/(0.150-x) = 1.76 × 10^-5#
#0.150/(1.76 × 10^"-5") = 8523 > 400#. ∴ #x ≪ 0.150##
#x^2 = 0.150 × 1.76 × 10^"-5" = 2.64 × 10^"-6"#
#x = sqrt(2.64 × 10^"-6") = 1.62 × 10^"-3"#
#["H"_3"O"^"+"] = xcolor(white)(l) "mol/L" = 1.62 × 10^"-3"color(white)(l) "mol/L"#
#"pH" = -log["H"_3"O"^"+"] = -log(1.62 × 10^"-3") = 2.79#
b) At 17.5 mL
This is the point of half-neutralization.
;:#"pH" = pK_"a" = -log(1.76 × 10^"-5") = 4.75#
c) At 34.5 mL
#color(white)(mmmmmm)"HA" +color(white)(m) "OH"^"-"color(white)(m) ⇌ color(white)(m)"A"^"-" + "H"_2"O"#
#"I/mmol":color(white)(ml)5.25color(white)(mml)5.175color(white)(mmmll)0#
#"C/mmol":color(white)(ll)"-5.175"color(white)(ml)"-5.175"color(white)(mm)"+5.175"#
#"E/mmol":color(white)(m)0.075color(white)(mm)0color(white)(mmmmll)5.175#
#"Initial moles of HA" = 0.0350 color(red)(cancel(color(black)("L"))) × "0.150 mol"/(1 color(red)(cancel(color(black)("L")))) = "0.005 25 mol" = color(red)(bb"5.25 mmol")#
#"Moles of NaOH added" = 0.0345 color(red)(cancel(color(black)("L"))) × "0.150 mol"/(1 color(red)(cancel(color(black)("L")))) = "0.005 175 mol" = "5.175 mmol"#
#"Moles of HA remaining" = ("5.25 -5.175) mmol" = "0.075 mmol"#
#"pH" = "p"K_"a" + log((["A"^"-"])/(["HA"])) = 4.75 + log((5.175 color(red)(cancel(color(black)("mol"))))/(0.075 color(red)(cancel(color(black)("mol"))))) = 4.75 + log(69.0) = 4.75 + 1.84 = 6.59#
d) At 35.0 mL
#color(white)(mmmmmm)"HA" +color(white)(m) "OH"^"-"color(white)(m) ⇌ color(white)(m)"A"^"-" + "H"_2"O"#
#"I/mmol":color(white)(ml)5.25color(white)(mml)5.25color(white)(mmmml)0#
#"C/mmol":color(white)(ll)"-5.25"color(white)(mm)"-5.25"color(white)(mlmm)"+5.25"#
#"E/mmol":color(white)(m)0color(white)(mmmm)0color(white)(mmmmmll)5.25#
You have a solution of 5.25 mmol of #"A"^"-"# in 70.0 mL.
#["A"^"-"] = "5.25 mmol"/"70.0 mL" = "0.0750 mol/L"#
#color(white)(mmmmmmm)"A"^"-" +color(white)(m) "H"_2"O"color(white)(m) ⇌ color(white)(m)"HA" + "OH"^"-"#
#"I/mmmol":color(white)(mml)0.0750color(white)(mmmmmmmmll)0color(white)(mml)0#
#"C/mmol":color(white)(mmmm)"-"xcolor(white)(mmmmmmmmm)"+"xcolor(white)(mll)"+"x#
#"E/mmol":color(white)(mml)0.0750 - xcolor(white)(mmmmmmml)xcolor(white)(mml)x#
#K_"b" = K_"w"/K_"a" = (1.00 × 10^"-14")/(1.76 × 10^"-5") = 5.68 × 10^"-10"#
#K_"b" = (["HA"]["OH"^"-"])/(["A"^"-"]) = x^2/(0.0750-x) = 5.68 × 10^"-10"#
#0.0750/(5.68×10^"-10") = 1.32 × 10^8 > 400#. ∴ #x ≪ 0.0750#
#x^2 = 0.0750 × 5.68 × 10^"-10" = 4.26 × 10^"-11"#
#x = sqrt(4.26 × 10^"-11") = 6.53 × 10^"-6"#
#["OH"^"-"] = 6.53 × 10^"-6" color(white)(l)"mol/L"#
#"pOH" = -log(6.53 × 10^"-6") = 5.19#
#"pH" = "14.00 - pOH" = 14.00 - 5.19 = 8.81#
e) At 35.5 mL
You are now adding excess moles of #"OH"^"-"#
#"Excess moles of OH"^"-" = 0.5 color(red)(cancel(color(black)("mL OH"^"-"))) × "0.150 mmol OH"^"-"/(1 color(red)(cancel(color(black)("mL OH"^"-")))) = "0.075 mmol OH"^"-"#
#["OH"^"-"] = "0.075 mmol"/"70.5 mL" = 1.06 × 10^"-3" "mol/L"#
#"pOH" = -log(1.06 × 10^"-3" ) = 2.97#
#"pH" = "14.00 - 2.97" = 11.03#
f) At 50.00 mL
#"Excess moles of OH"^"-" = 15.0 color(red)(cancel(color(black)("mL OH"^"-"))) × "0.150 mmol OH"^"-"/(1 color(red)(cancel(color(black)("mL OH"^"-")))) = "2.25 mmol OH"^"-"#
#["OH"^"-"] = "2.25 mmol"/"85.0 mL" = "0.0265 mol/L"#
#"pOH" = -log(0.0265) = 1.58#
#"pH" = "14.00 - 1.58" = 12.42#
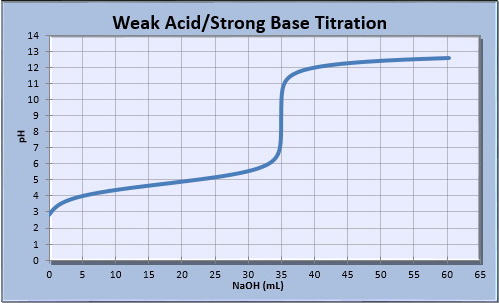
Your calculated values should match the titration curve below.