A 6 kg shell is fired with a 30° angle,v= 40 m/s. At the highest point it devides into 2 parts,one 2 kg and the other 4 that move in the horizontal line and 2 kg hits the ground at the start point.where the 4 kg piece hits the ground?

2 Answers
ali ergin
Feb 10, 2018

#"please check the math operations."#

Explanation:

enter image source here

  • We will use the principle of momentum conservation to solve the problem.
  • In the solution of the problem, we must assume that the conditions are ideal and that there is no energy loss.
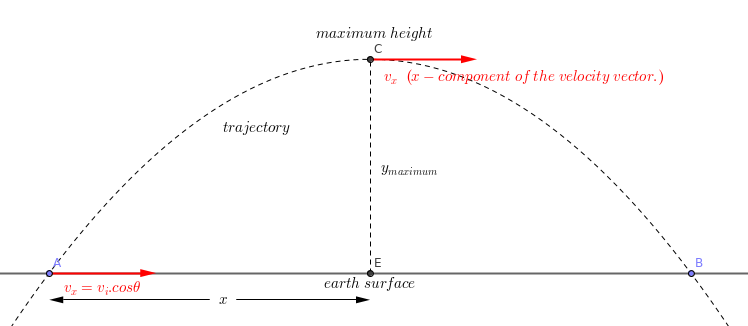
  • Suppose that C is the maximum height. At this point, the object instantaneously has only a horizontal velocity component.

  • When the object is at point C, it only has instant horizontal momentum.

  • momentum vector and direction are seen below.

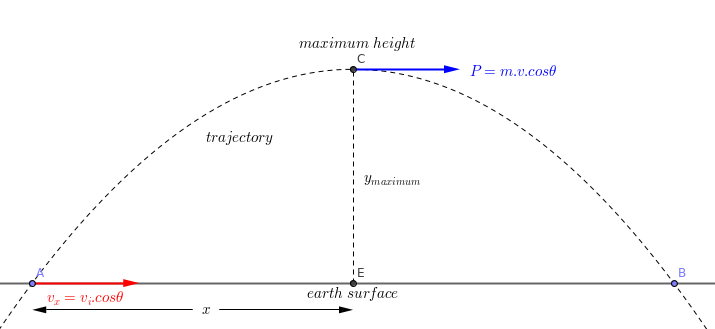
enter image source here

#vec P=m. vec v_x#

#P=m v *cos theta=6*40*0.866=207.85" "kg*m s^-1#

  • we have to rethink the momentum of each piece when the bullet is divided into two.
  • the vectorial sum of the vertical momentum of the parts is zero.Because the bullet only had horizontal momentum.
  • Both parts of the bullet must have horizontal momentum.
  • The momentum vectors for the part are given below.

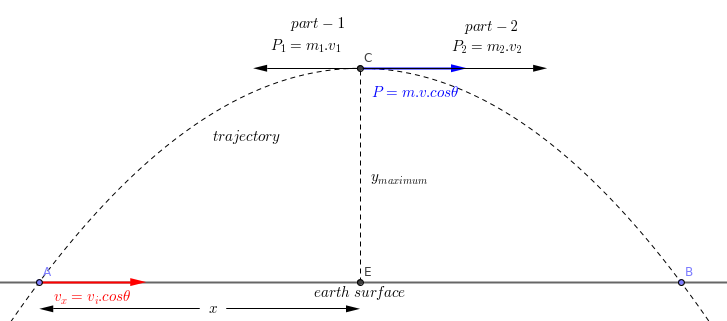
enter image source here

#vec P=vec P_1+ vec P_2#

  • Because the first part is returned to its original position, the velocity of this part is equal to and opposite to the horizontal velocity component.

#P_1=m_1v cos theta=2*40*0.866=69.28" "kg.ms^-1#

  • We can find the momentum of the second part.

#207.85=-69.28+P_2#

#P_2=207.85+69.28=277.13" "kg*ms^-1#

  • Now we can find the velocity of the second part.

#P_2=m_2 v_2#

#277.13=4 v_2#

#v_2=(277.13)/4=69.28" " ms^-1#

  • Objects thrown horizontally from the same height reach equally long.

#t=(v_i*sin theta)/g=(40*0.5)/(9.81)=2.04" "sec#

#x=v_i*t*cos theta=40*2.04*0.866=76.67 " "m#

#x_1=v_2*t=69.28*2.04=141 .33" "m#

#AM=x+x_1=76.67+141.33=218" "m#

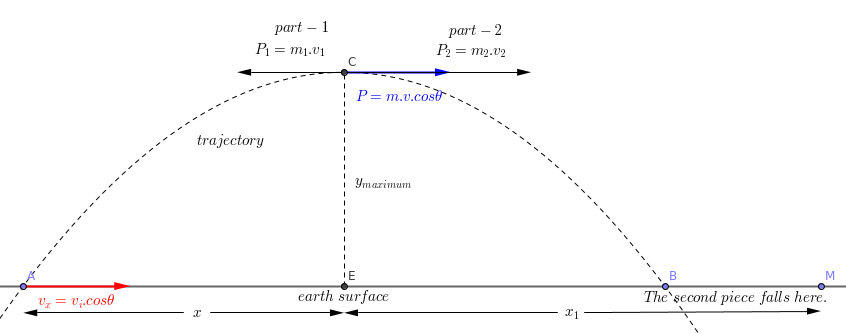
enter image source here

  • falls 218 meters from the point where it is thrown.

P dilip_k
Feb 15, 2018

drawn

  • Mass of the shell #m=6kg#
  • Velocity of projection #V=40m"/"s#
  • Angle of projection #theta=30^@#
  • Mass of smaller part after the division of the shell #m_1=2kg#
  • Mass of larger part after the division of theshell #m_2=4kg#

  • The horizontal component of velocity of projection #Vcostheta#

  • The vertical component of velocity of projection #Vsintheta#

If time of flight be T then

#0=VsinthetaT-1/2gT^2#

#=>T=(2Vsintheta)/g#, where #g=9.8ms^-2# is the acceleration due to gravity

The range #R# of the projectile ie the horizontal displacement of the projectile during time of flight #T# is

#R=VcosthetaxxT==Vcosthetaxx(2Vsintheta)/g=(v^2sin2theta)/g#

Hence #color(red)(R=(40^2sin(2*30^@))/9.8=(40^2sqrt3/2)/9.8~~141.4m#

1st method of calculation

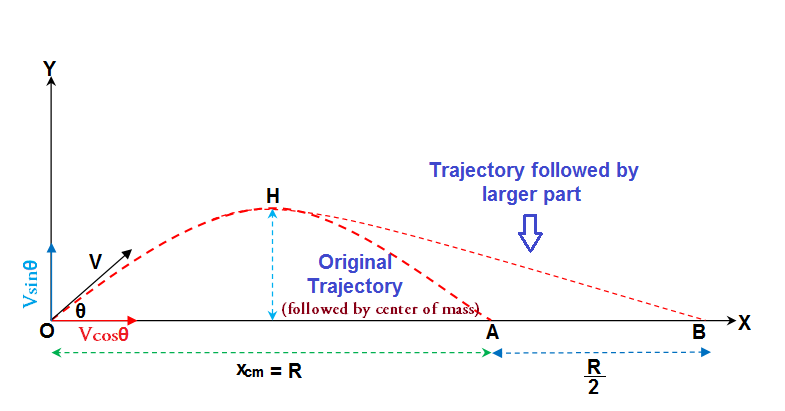
This is based on the fact that the center of mass of the projectile follows the same trajectory even if it is divided in to two or more parts due to explosion at any point during its time of flight and so suffers same horizontal displacement after completion of time of flight (T)

So if #x_1 and x_2# are the final horizontal displacements of smaller and larger parts of mass #m_1 and m_2# respectively from point of launching #O# then the displacement #(x_"cm")# of their center of mass will be given by

#x_"cm"=(m_1x_1+m_2x_2)/(m_1+m_2)#

#=>x_"cm"=(m_1x_1+m_2x_2)/m#

By the condition of the problem

#x_"cm"=R and x_1=0#

So #(m_1x_1+m_2x_2)/m=R#

#=>(2*0+4*x_2)/6=R#

#=>x_2=3/2R=3/2xx141.4~~212m#

2nd method of calculation

This method is based on the principle of conservation of momentum. The explosion occurs at the highest position (H) of the projectile and the smaller part of the projectile of mass #m_1=2kg# after explosion retraces the path (HO) and finally reaches (after time #T/2 # ) at the launching point (O) .

At the highest point just before the moment of explosion the projectile has got only horizontal component of its velocity #Vcostheta# and it has got momentum #color (green)(mVcostheta)#

After division into two parts at highest point #H# the smaller part of mass #m_1 # retraces the path of the projectile and reaches at the launching point O after same #T/2#s, the time of ascent . So it must have attained the horizontal velocity of same magnitude in opposite direction ie #-Vcostheta# after division. Hence its momentum just after the division should be #color(red)(-m_1Vcostheta)#. If lager part of mass #m_2# gains velocity #V'# in horizontal direction just after the division then by the principle of conservation of momentum we can write

#color(green)(mVcostheta)=color(red)(-m_1Vcostheta)+color(blue)(m_2V')#

#=>6Vcostheta=-2Vcostheta+4V'#

#=>color(blue)(V'=2Vcostheta)#

So Total horizontal displacement of the larger part
= displacement before explosion during 1st half of time of flight + displacement of larger part after explosion during 2nd half of time of flight

#=VcosthetaxxT/2+V'xxT/2#

#=VcosthetaxxT/2+2VcosthetaxxT/2#

#=3/2xxVcosthetaxxT#

#=3/2xxR#

#=3/2xx141.4m~~212m#

Related questions
Impact of this question
1383 views around the world
You can reuse this answer
Creative Commons License