Question

A 600 K piece of metal would emit radiation at a peak wavelength of what?

Answer 1

`lamda_"max" = "5000 nm"`

Explanation:

For an object that emits black-body radiation, the peak wavelength is simply the wavelength at which the intensity of the emitted radiation is at its maximum value.

Now, black-body radiation is a type of electromagnetic radiation emitted by a black body that's held at a constant temperature. The important thing to realize about black-body radiation is that its intensity depends exclusively on the absolute temperature of the body.

The relationship between the maximum intensity of the black-body radiation emitted by an object and the wavelength at which it occurs is given by the Wien displacement law equation

`color(blue)(lamda_"max" = b/T)" "`, where

`lamda_"max"` - the wavelength at which the intensity of the radiation is maximum
`b` - the Wien displacement constant, usually given as `2.89777 * 10^(-3)"m K"`
`T` - the absolute temperature of the object

In your case, the absolute temperature of the metal is said to be equal to `"600 K"`. This means that its peak wavelength will be equal to

`lamda_"max" = (2.89777 * 10^(-3) "m" color(red)(cancel(color(black)("K"))))/(600color(red)(cancel(color(black)("K")))) = 4.83 * 10^(-6)"m"`

Expressed in nanometers and rounded to one sig fig, the number of sig figs you have for the temperature of the metal, the answer will be

`lamda_"max" = color(green)("5000 nm")`

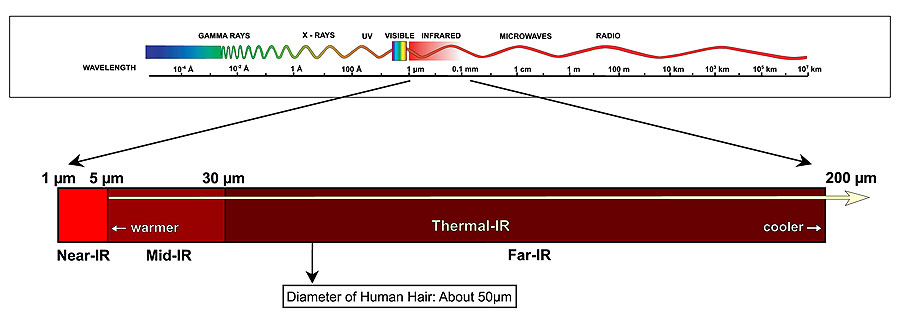
This wavelength places the radiation in the infrared region of the electromagnetic spectrum. More specifically, this wavelength corresponds to the Far-IR region.