Question

A balanced lever has two weights on it, one with mass `2 kg` and one with mass `8 kg`. If the first weight is `4 m` from the fulcrum, how far is the second weight from the fulcrum?

Answer 1

`1m`

Explanation:

The concept that comes into use here is torque. For the lever to not tip over or rotate, it must have a net torque of zero.

Now, the formula of torque is `T=F*d`.

Take an example to understand, if we hold a stick and attach a weight at the front of the stick, it doesn't seem too heavy but if we move the weight to the end of the stick, it seems a lot heavier. This is because the torque increases.

Now for the torque to be same,
`T_1=T_2`

`F_1*d_1=F_2*d_2`

The first block weighs 2 kg and exerts approximately `20N` of force and is at a distance of 4m

The first block weighs 8 kg and exerts approximately `80N`

Putting this in the formula,

`20*4=80*x`

We get that x= 1m and hence it must be placed at a distance of 1m

Answer 2

The distance is `=1m`

Explanation:

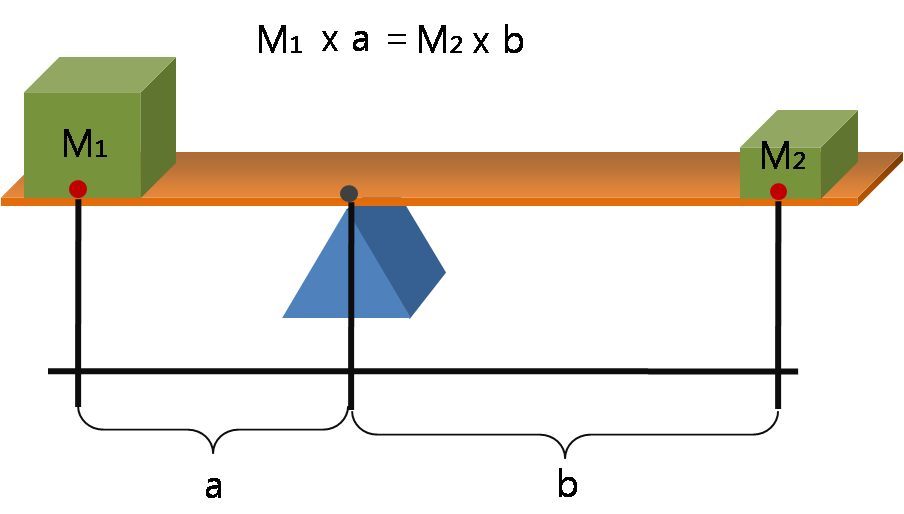www.thoughtco.com

The mass `M_1=2kg`

The mass `M_2=8kg`

The distance `a=4m`

Taking moments about the fulcrum

`M_1xxa=M_2xxb`

The distance is

`b=(M_1xxa)/(M_2)=(2*4)/(8)=1m`