A balanced lever has two weights on it, the first with mass #5 kg # and the second with mass #3 kg#. If the first weight is # 6 m# from the fulcrum, how far is the second weight from the fulcrum?
1 Answer
10 meters
Explanation:
Imagine a see-saw where two people sit on either end.
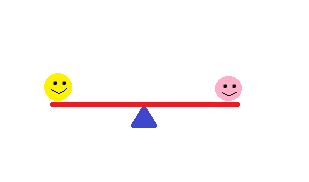
Assuming the two smileys weigh the same amount and are the same distance from the center of the see-saw (the fulcrum), the see-saw is balanced.
Now imagine, the pink smiley and her best friend sit together on her end of the see-saw. What happens? The pinks' side will go down, while the boy's side goes up!
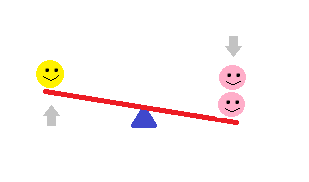
Next, let's say the pink's scoot up the see-saw so that they are sitting half-way between the end of their side and the fulcrum. What happens now?
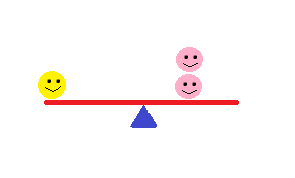
They're balanced again! So, we've changed two variables: weight and distance. The ability to rotate around a fulcrum, torque, is dependent on force and distance.
If a system is not rotating, clockwise and counter-clockwise rotation are balanced:
In our case:

