Question

A ball with a mass of `120 g` is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of `15 (kg)/s^2` and was compressed by `3/5 m` when the ball was released. How high will the ball go?

Answer 1

The height reached by the ball is `=2.30m`

Explanation:

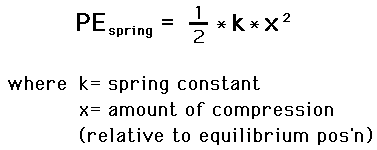
The spring constant is `k=15kgs^-2`

The compression of the spring is `x=3/5m`

The potential energy stored in the spring is

`PE=1/2kx^2=1/2*15*(3/5)^2=2.7J`

This potential energy will be converted to kinetic energy when the spring is released and to potential energy of the ball

`KE_(ball)=1/2m u^2`

Let the height of the ball be `=h`

The acceleration due to gravity is `g=9.8ms^-2`

Then ,

The potential energy of the ball is `PE_(ball)=mgh`

Mass of the ball is `m=0.120kg`

`PE_(ball)=2.7=0.120*9.8*h`

`h=2.7/(0.120*9.8)`

`=2.30m`

The height reached by the ball is `=2.30m`

Answer 2

`2.293\ m`

Explanation:

Assuming spring to be perfectly elastic, when the ball is released, the entire elastic energy of spring `1/2kx^2` is transferred to the ball in form of kinetic energy `1/2mv^2`
Where, `k` is spring constant,

`x` initial compression of spring

`m` is mass of ball

`u` is the velocity of ball when it is thrown vertical upward

hence, we have

`\text{K.E. of ball}=\text{elastic energy of spring}`

`1/2(0.120)u^2=1/2(15)(3/5)^2`

`u^2=135/3`

`u=\sqrt{135/3}`

Now, using third equation of motion:

`v^2=u^2+2as`

For the motion against gravity, we have `a=-g=-9.81\ \text{m/s}^2`, initial velocity `u=\sqrt{135/3}` & final velocity `v` at the maximum height `s=h` becomes zero i.e. `v=0`

hence, we have

`0^2=(\sqrt{135/3})-2(9.81)h`

`h=\frac{135}{3\cdot 19.62}`

`=2.293\ m`