A ball with a mass of #125 g# is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of #8 (kg)/s^2# and was compressed by #2/5 m# when the ball was released. How high will the ball go?

Question

1319 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-08T05:30:08

The height is #=0.52m#

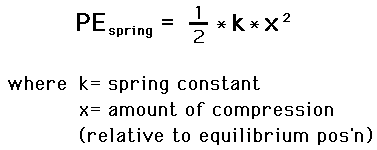
enter image source here

The spring constant is #k=8kgs^-2#

The compression is #x=2/5m#

The potential energy is

#PE=1/2*8*(2/5)^2=16/25=0.64J#

This potential energy will be converted to kinetic energy when the spring is released

#KE=1/2m u^2#

The initial velocity is #=u#

#u^2=2/m*KE=2/m*PE#

#u^2=2/0.125*0.64=10.24#

#u=sqrt10.24=3.2ms^-1#

Resolving in the vertical direction #uarr^+#

We apply the equation of motion

#v^2=u^2+2ah#

At the greatest height, #v=0#

and #a=-g#

So,

#0=10.24-2*9.8*h#

#h=10.24/(2*9.8)=0.52m#