A ball with a mass of #3 kg # and velocity of #5 m/s# collides with a second ball with a mass of #7 kg# and velocity of #- 1 m/s#. If #25%# of the kinetic energy is lost, what are the final velocities of the balls?
1 Answer
Velocity of 3 kg ball: v₁ = 2.8 m s⁻¹ to the left
Velocity of 7 kg ball: v₂ = 2.3 m s⁻¹ to the right
Explanation:
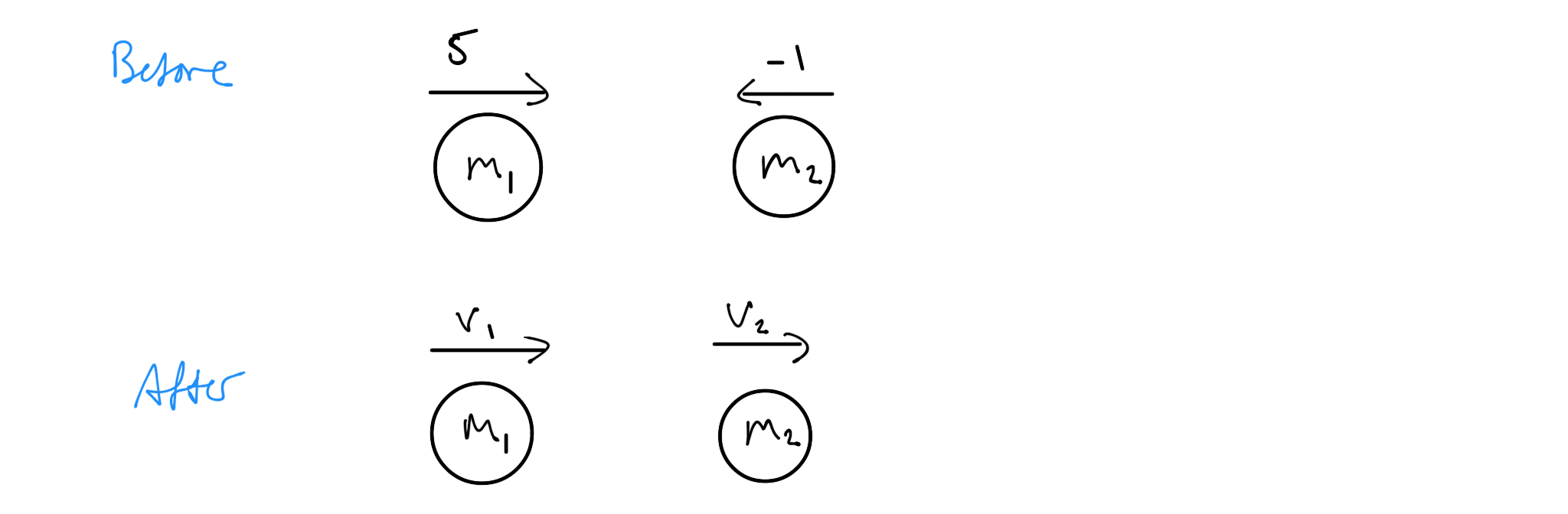
m₁ = 3 kg
u₁ = 5 m s⁻¹
m₂ = 7 kg
u₂ = -1 m s⁻¹
Conservation of momentum:
Substitute values into equation:
Conservation of energy:
If 25% of the kinetic energy is lost then the final kinetic energy is equal to 75% of the initial kinetic energy.
⇒
Substitute values into equation:
Solve the simultaneous equations ① and ②:
From ①:
Substitute for v₁ in equation ②:
⇒
⇒
Use an equation to solve for the factors of the quadratic, i.e. this will give possible solutions for v₂.
Solution 1:
Solution 2:
Substitute each of those solutions into equation 1 to find possible solutions for v₁:
E.g.
Now interpret the results qualitatively (in words):
Solution set 1 (v₁ = -2.786 m s⁻¹ and v₂ = 2.337 m s⁻¹) : ball 1 reverses direction at a lower velocity and ball 2 reverses direction at a faster velocity.
Solution set 2 (v₁ = 4.386 m s⁻¹ and v₂ = -0.7367 m s⁻¹) : ball 1 slows down slightly and ball 2 also slows down slightly, they both continue in the same direction.
Whilst the two solutions are mathematically satisfactory we can see from a qualitative analysis that solution two is physically impossible. The two balls were initially moving toward each other, they cannot both just slow down slightly after colliding and continue in the same direction unless they magically pass through each other.
For that reason the solution to the problem is that the final velocities are:
v₁ = -2.8 m s⁻¹ (i.e. 2.8 m s⁻¹ to the left)
v₂ = 2.3 m s⁻¹ (2.3 m s⁻¹ to the right)

