A ball with a mass of #450 g# is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of #12 (kg)/s^2# and was compressed by #4/3 m# when the ball was released. How high will the ball go?
1 Answer
May 8, 2017
The height is
Explanation:
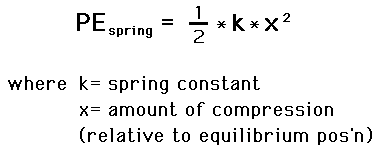
The spring constant is
The compression is
The potential energy is
This potential energy will be converted to kinetic energy when the spring is released
The initial velocity is
Resolving in the vertical direction
We apply the equation of motion
At the greatest height,
and
So,

