Question

A ball with a mass of `480 g` is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of `18 (kg)/s^2` and was compressed by `6/5 m` when the ball was released. How high will the ball go?

Answer 1

`1.55m`

Explanation:

Lets consider the conservation of energy:

Initially:

Potential energy due to the compression of spring = `1/2kx^2`

Finally,

Gravitation potential energy = `mgh`

hence,

`mgh = 1/2 kx^2`

`=> h = (kx^2)/(2mg) = (18*(6/5)^2)/(2*0.48*9.8) = 2.75m`

Notice, because I have not considered any gravitational potential energy initially, this height is from the compressed position of the object.

So, from the unstressed spring: `(2.75-1.2)m = 1.55m`

Answer 2

`2.75m`, rounded to two decimal places.
height is measured from the compressed position of the spring.

Explanation:

We know that Elastic potential energy of an elongated/compressed spring is given by
`PE=1/2kx^2`
where `k` is spring constant and `x` is the deformity of the spring. Compression in our problem.


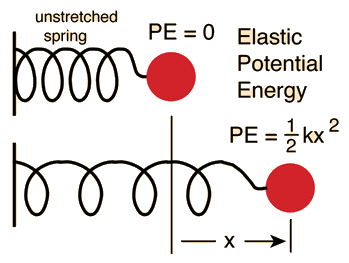
Substituting given values in the above expression
`PE=1/2xx18xx(6/5)^2J`
`PE=12.96J`.....(1)
Assuming that the transfer of this elastic potential energy from the contraption to the ball which is thrown upwards is elastic and all the energy is converted into the kinetic energy of the ball.

Once the ball is in air, gravity starts pulling it down. At height `h`, the ball will become stationary and thereafter start its downwards fall. Again assuming that air friction is negligible, at height `h`

Gravitational potential energy `=mgh`,
Inserting given value of mass and using `g=9.81ms^-2`
Gravitational potential energy `=0.48xx9.81h` ....(2)

This is the point where all the initial kinetic energy of the ball imparted by the spring contraption gets converted into Gravitational potential energy. Equating (1) and (2) and solving for `h`
`12.96=0.48xx9.81h`
`h=(12.96)/(0.48xx9.81)`
`h=2.75m`, rounded to two decimal places.
height is measured from the compressed position of the spring.