Question

A ball with a mass of `80 g` is projected vertically by a spring loaded contraption. The spring in the contraption has a spring constant of `16 (kg)/s^2` and was compressed by `1/5 m` when the ball was released. How high will the ball go?

Answer 1

I tried this but check my maths.

Explanation:

We can consider:

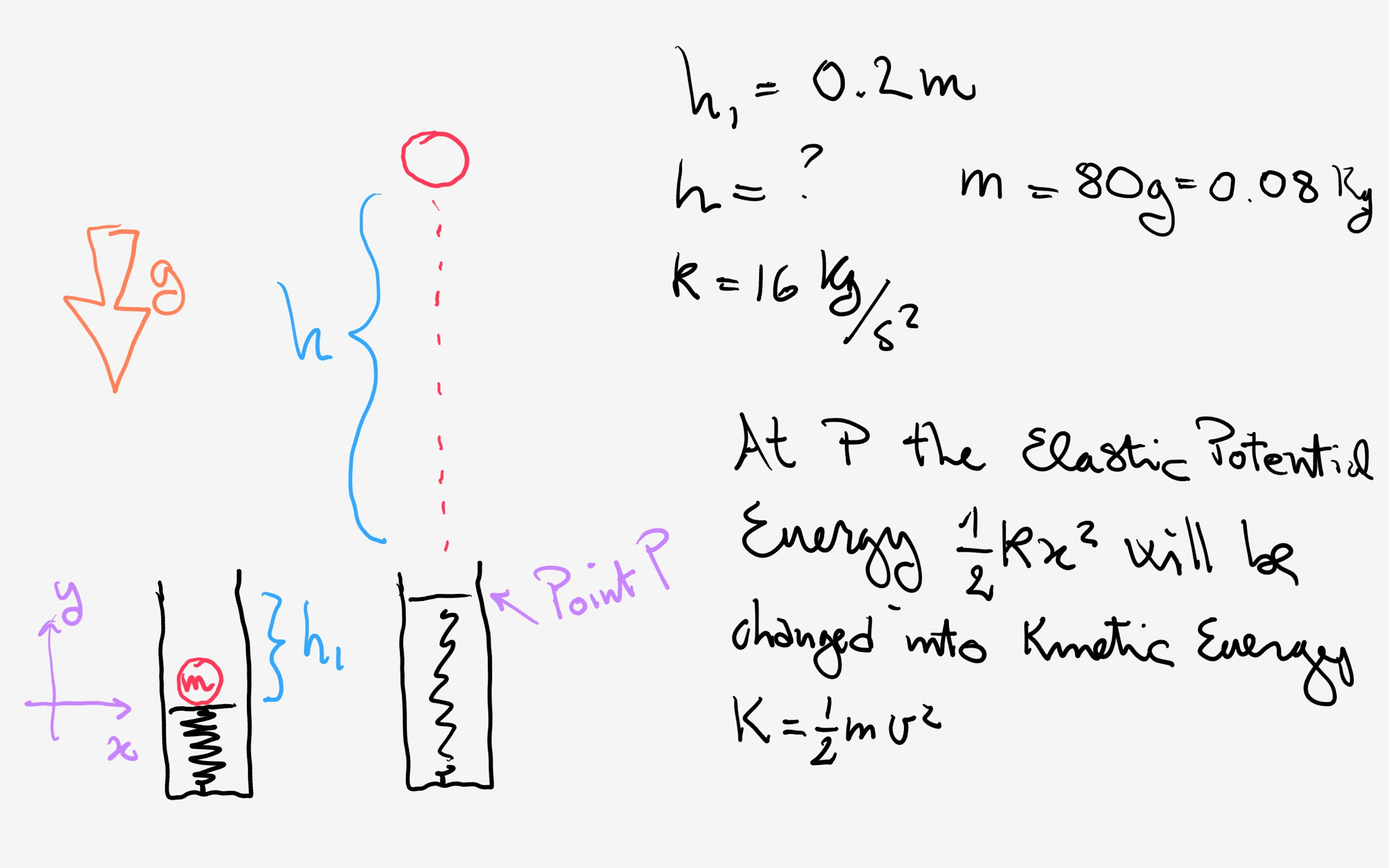
So basically we can write:
`1/2kx^2=1/2mv^2`
`v=sqrt((kx^2)/m)=sqrt(8)=2.8m/s`

We now use the kinematic relationship:
`v_f^2=v_i^2+2ah`
With `a=` acceleration of gravity downwards and `v_f=0` for the final velocity;
`0=8-(2*9.8*h)`
`h=8/(2*9.8)=0.4m`
If we consider also the initial compression, the total vertical distance should be:
`h+h_1=0.4+0.2=0.6m`