A balloon has a volume of 253.2 L at 356 K. The volume of the balloon is decreased to 165.4 L. What is the new temperature?
1 Answer
Explanation:
Before doing any calculation, try to predict what you expect the new temperature to be relative to the initial temperature.
In your case, number of moles of gas and pressure are kept constant. When this is the case, volume and temperature have a direct relationship - this is known as Charles' Law.
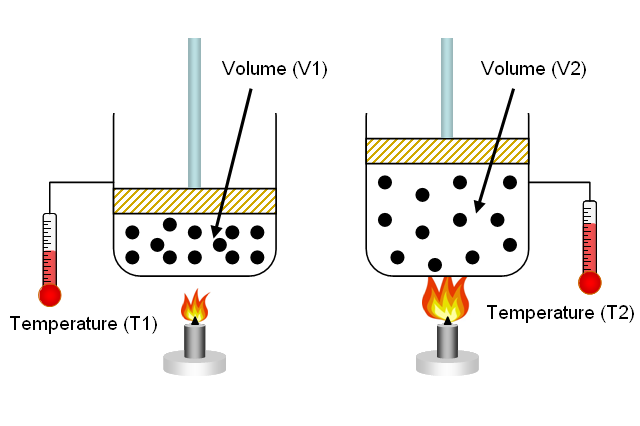
So, why is this the case?
As you know, the pressure of a gas is determined by the force with which its molecules collide with the walls of the balloon.
Temperature is simply a measure of the average kinetic energy of the gas molecules. When a gas is heated, its molecules move faster.
This will result in more powerful and more frequent collisions with the walls of the balloon, which in turn will cause the pressure to increase.
However, when pressure is kept constant, this increase in the average kinetic energy of the gas molecules causes an increase in the volume of the balloon.
Simply put, increasing the volume counteracts the increase in temperature, keeping pressure constant. A bigger volume implies more room for the molecules to move in, which will result in less frequent collisions between the gas molecules and the walls of the balloon.
In your case, the volume actually decreases. This means that you can expect the temperature of the gas molecules to be lower, since reducing volume while decreasing the average kinetic speed of the molecules will keep pressure constant.
Mathematically, this is written as
#color(blue)(V_1/T_1 = V_2/T_2)" "# , where
In your case, you will have
#T_2 = V_2/V_1 * T_1#
#T_2 = (165.4 color(red)(cancel(color(black)("L"))))/(253.2color(red)(cancel(color(black)("L")))) * "356 K" = "232.55 K"#
Rounded to three sig figs, the number of sig figs you have for the initial temperature of the gas, the answer will be
#T_2 = color(green)("233 K")#
Indeed, our prediction turned out to be correct,

